Table of Contents
ToggleDifficulty: Medium, Asked-in: Amazon, Microsoft, Adobe, Google.
Problem Statement
The Least Recently Used (LRU) cache eviction policy is a caching strategy that removes the least recently accessed cache entries first when the cache capacity is reached. LRU caching works by keeping track of when each entry was last used. The items are sorted based on the time they were last accessed, with the most recently used items at the front and least recently used items at the end. When the cache fills up, the algorithm discards the least recently used entries first to make space for caching new data. This ensures that the cache contains the most frequently accessed items, while rarely used entries are removed to free up space.
Our goal is to design and implement a data structure for a Least Recently Used (LRU) cache.
Implement the LRUCache class with following functions:
- LRUCache(int capacity): Initializes the LRU cache with positive size capacity.
- int get(int key): Return the value of the key if the key exists. Otherwise, return -1.
- void put(int key, int value): Update the value of the key if the key exists. Otherwise, add the key-value pair to the cache. If the number of keys exceeds the capacity from this operation, evict the least recently used key.
Constraints:
- The functions
getandputmust each run inO(1)average time complexity.
Example:
Input
["LRUCache", "put", "put", "get", "put", "get", "put", "get", "get", "get"]
[[2], [1, 1], [2, 2], [1], [3, 3], [2], [4, 4], [1], [3], [4]]
Output
[null, null, null, 1, null, -1, null, -1, 3, 4]
Explanation
LRUCache lRUCache = new LRUCache(2);
lRUCache.put(1, 1); // cache is {1=1}
lRUCache.put(2, 2); // cache is {1=1, 2=2}
lRUCache.get(1); // return 1
lRUCache.put(3, 3); // LRU key was 2, evicts key 2, cache is {1=1, 3=3}
lRUCache.get(2); // returns -1 (not found)
lRUCache.put(4, 4); // LRU key was 1, evicts key 1, cache is {4=4, 3=3}
lRUCache.get(1); // return -1 (not found)
lRUCache.get(3); // return 3
lRUCache.get(4); // return 4
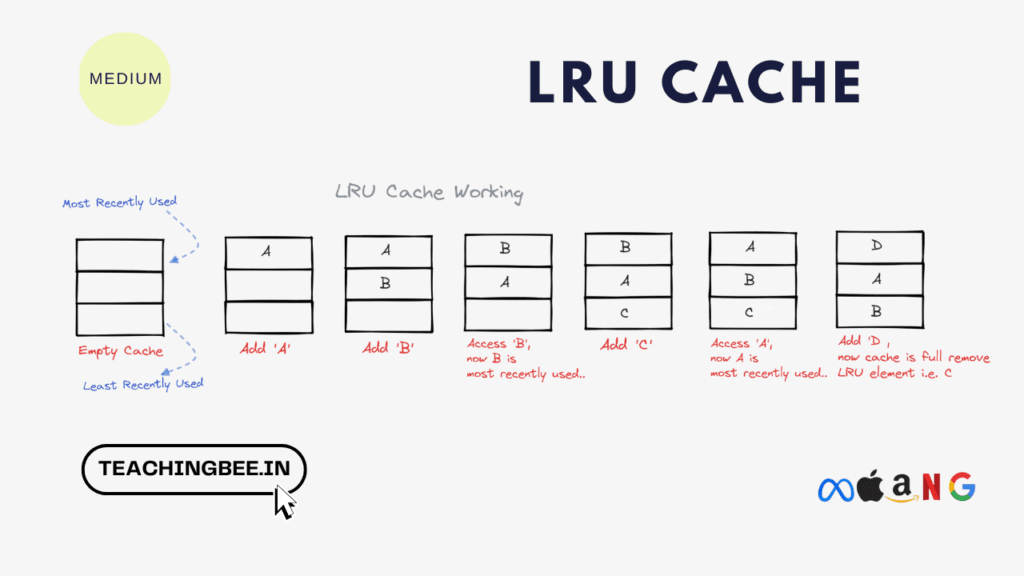
Let’s understand the problem via a diagram
Imagine an LRU cache with a capacity of 3 items:
- Initial State: Cache is empty.
- Add ‘A’: Cache becomes: A
- Add ‘B’: Cache becomes: B, A (B is more recent than A)
- Add ‘C’: Cache becomes: C, B, A
- Access ‘A’: Cache becomes: A,C,B (B becomes the most recent)
- Add ‘D’: Cache is full, so ‘A’ (the least recently used item) is evicted. Cache becomes: D, C, B.

Solution
Intuition
The problem can be efficiently tackled by combining a doubly linked list and a hash map. The doubly linked list allows us to quickly move nodes to the head (to mark an item as recently used) and remove nodes from the tail (to remove the least recently used items), while the hash map allows for quick access to individual nodes.
Why Use a Doubly Linked List and a HashMap?
To implement a Least Recently Used (LRU) cache, we need fast lookups to access cache items, and also a way to track the order of access. For this, we can use a hashmap paired with a doubly linked list. The hashmap allows O(1) lookup time to check if an item is in the cache. It stores key-value pairs mapping the cache items to nodes in the linked list. The doubly linked list orders the items by recency – with most recently used item at the head and least recently used at the tail. When a new item is accessed, it can be moved to the head in O(1) time by reordering the links.
On a cache hit, we move the node to the head of the list, updating its position. When adding new items in a full cache, we evict the tail node and add the new item at the head. The HashMap is updated to delete and add the key-node mappings. This gives us fast O(1) lookups via the HashMap, along with tracking of order and cheap reordering using the doubly linked list. The combination provides an efficient way to implement LRU cache eviction when the cache capacity is reached.
- Doubly Linked List: The LRU cache needs a mechanism to track the order of usage of keys, with the ability to quickly identify and remove the least recently used item and quickly add/move items to the front when they are used or added. A doubly linked list is perfect for this: items can be efficiently added to the front (head) and removed from the back (tail).
- HashMap: This provides constant time complexity for fetching a node associated with a key. When a get or put operation is called with a key, we don’t want to traverse our doubly linked list looking for nodes associated with that key. Instead, the map lets us jump directly to the relevant node.
In combination, these data structures allow the LRU cache to function efficiently, ensuring operations are executed in constant time. The HashMap guarantees quick access, while the doubly linked list maintains the order of use.
LRU Cache Algorithm
Data Structures:
- A Doubly Linked List (DDL) to store the cache items. Each node will have a key and a value.
- A Hash Map where the key is the cache item’s key and the value is a reference to the node in the DDL.
Initialization:
- Set the maximum capacity of the cache.
- Initialize an empty DDL.
- Initialize an empty Hash Map.
Operations:
1. GET(key):
- If the key is present in the Hash Map:
a. Fetch the node using the Hash Map.
b. Move the node to the front of the DDL (indicating recent use).
c. Return the value of the node. - Else:
- Return “Not Found” or a similar indicator.
2. PUT(key, value):
- If the key is already present in the Hash Map:
a. Update the node’s value.
b. Move the node to the front of the DDL. - Else:
- If the DDL has reached its maximum capacity:
i. Remove the node from the end of the DDL (this is the least recently used item).
ii. Remove the corresponding entry from the Hash Map. - Add a new node with the key and value to the front of the DDL.
- Add a corresponding entry in the Hash Map.
- If the DDL has reached its maximum capacity:
Two significant operations of LRU Cache are :
- GET Operation
- PUT Operation
Let’s look into each of these in detail.
GET Operation
The get operation needs to fetch the value for a given key if it exists in the cache. If the key is found, then this key has been recently used, and we need to move it to the front (head) of the doubly linked list to reflect this. If the element is not found, we return -1. The time complexity for this operation is O(n), as we may need to traverse the entire linked list to find the desired element.
// GET Operation: LRU Cache LeetCode Problem
public int get(int key) {
// Initialize the result as -1 (default value if the key is not found).
int result = -1;
// Attempt to retrieve the node associated with the given key from the map.
Node node = map.get(key);
if (node != null) {
// If the node exists (key is in the cache):
// 1. Retrieve the value associated with the node.
result = node.value;
// 2. Move the accessed node to the front of the linked list (MRU position)
// since it is now the most recently used.
moveToHead(node);
}
// Return the result (either the value associated with the key or -1 if not found).
return result;
}Here, the map.get(key) operation fetches the node corresponding to the key in constant time. If the node exists, we move this node to the front of the list using moveToHead(node).
PUT Operation
The put operation has a bit more going on:
- If the key already exists in the cache, we update its value and move it to the front of the list, indicating it’s the most recently used.
- If the key doesn’t exist:
- First, we check if adding this new key would exceed our cache’s capacity.
- If it does, we need to evict the least recently used item, which will be at the end (tail) of our list and removing it from the hash map.
- After possibly evicting, we then add the new key-value pair.
// Put Operation: LRU Cache LeetCode Problem
public void put(int key, int value) {
// Attempt to retrieve the node associated with the given key from the map.
Node node = map.get(key);
if (node != null) {
// If the node already exists (key is in the cache):
// 1. Update the value of the existing node with the new value.
node.value = value;
// 2. Move the updated node to the front of the linked list (MRU position)
// since it is now the most recently used.
moveToHead(node);
} else {
// If the node doesn't exist (key is not in the cache):
if (map.size() >= capacity) {
// If the cache has reached its capacity:
// 1. Remove the least recently used key from the map.
map.remove(tail.prev.key);
// 2. Remove the least recently used node from the linked list.
removeNode(tail.prev);
}
// Create a new node to represent the key-value pair.
Node newNode = new Node();
// Set the key and value for the new node.
newNode.key = key;
newNode.value = value;
// 3. Add the new node to the map, associating it with the key.
map.put(key, newNode);
// 4. Add the new node to the front of the linked list (MRU position)
// since it is the most recently used.
addNode(newNode);
}
}Complete Java Implementation
// LRU Cache LeetCode Problem Java Solution
import java.util.*;
class LRUCache {
// Inner class representing a doubly linked list node
class Node {
int key;
int value;
Node prev;
Node next;
}
private final int capacity;
private final Map<Integer, Node> map = new HashMap<>();
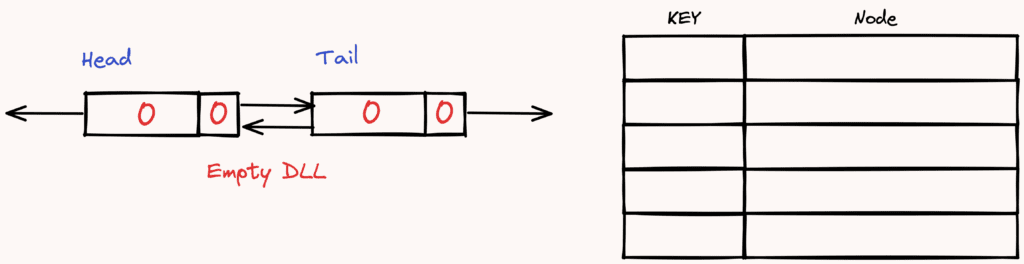
private final Node head = new Node(); // Dummy head and tail nodes to avoid edge cases in doubly linked list
private final Node tail = new Node();
public LRUCache(int capacity) {
this.capacity = capacity;
head.next = tail;
tail.prev = head;
}
public int get(int key) {
int result = -1;
Node node = map.get(key);
if (node != null) {
result = node.value;
moveToHead(node); // Move the accessed node to the front (MRU position)
}
return result;
}
public void put(int key, int value) {
Node node = map.get(key);
if (node != null) {
node.value = value; // Update the existing node's value
moveToHead(node); // Move the updated node to the front (MRU position)
} else {
if (map.size() >= capacity) {
map.remove(tail.prev.key); // Remove the least recently used (LRU) node from both map and linked list
removeNode(tail.prev);
}
Node newNode = new Node(); // Create a new node for the key-value pair
newNode.key = key;
newNode.value = value;
map.put(key, newNode); // Add the new node to the map
addNode(newNode); // Add the new node to the front (MRU position) of the linked list
}
}
private void moveToHead(Node node) {
removeNode(node); // Remove the node from its current position
addNode(node); // Add the node to the front (MRU position)
}
private void removeNode(Node node) {
Node prevNode = node.prev;
Node nextNode = node.next;
prevNode.next = nextNode;
nextNode.prev = prevNode;
}
private void addNode(Node node) {
Node headNext = head.next;
node.next = headNext;
headNext.prev = node;
head.next = node;
node.prev = head;
}
public static void main(String[] args) {
LRUCache cache = new LRUCache(2);
cache.put(1, 1);
cache.put(2, 2);
System.out.println(cache.get(1)); // returns 1
cache.put(3, 3); // evicts key 2
System.out.println(cache.get(2)); // returns -1 (not found)
cache.put(4, 4); // evicts key 1
System.out.println(cache.get(1)); // returns -1 (not found)
System.out.println(cache.get(3)); // returns 3
System.out.println(cache.get(4)); // returns 4
}
}Output Explanation
Output Explanation:
LRUCache(2)initializes an LRU cache with a capacity of 2.

put(1, 10)adds the key-value pair(1, 1)to the cache.put(2, 23)adds the key-value pair(2, 2)to the cache.
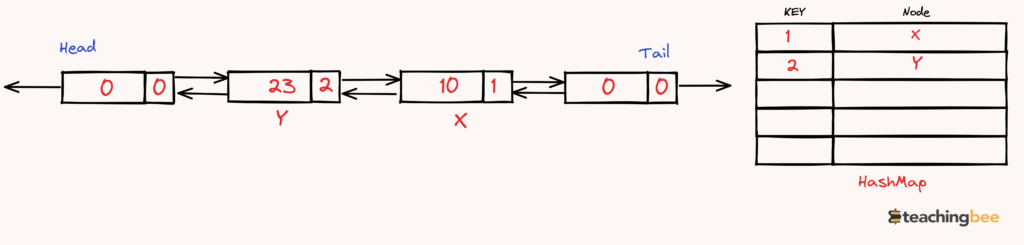

get(1)retrieves the value for key1, which is1, and this moves key1to the front of the list as the most recently accessed.
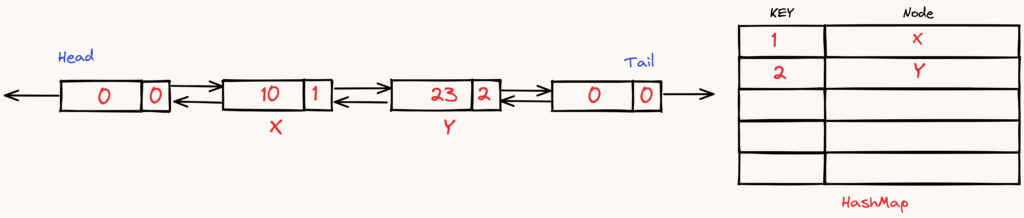

put(3, 13)attempts to add the key-value pair(3, 3)to the cache. However, the cache is full, so it evicts the least recently accessed key, which is2.
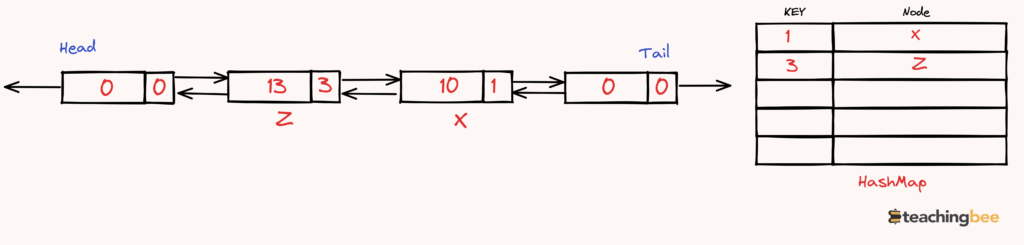

get(2)tries to retrieve the value for key2, but it was just evicted, so this returns-1.put(4, 25)adds the key-value pair(4, 4)to the cache. Since adding this key-value pair will exceed the capacity, it evicts the least recently accessed key, which is now1(even though it was accessed in step 4, it’s less recent than the access of key3in step 5).get(1)tries to retrieve the value for key1, but it was evicted in the previous step, so this returns-1.get(3)retrieves the value for key3, which is3.get(4)retrieves the value for key4, which is4.
I hope You liked the post ?. For more such posts, ? subscribe to our newsletter. Try out our free resume checker service where our Industry Experts will help you by providing resume score based on the key criteria that recruiters and hiring managers are looking for.