Table of Contents
ToggleIn this article we will solve Combination Sum LeetCode Problem which is a very good backtracking question.
Difficulty: Medium, Asked-in: Amazon, Adobe.
Problem Statement
Given an array of distinct integers and a target, you have to return the list of all unique combinations where the chosen numbers sum to target. You may return the combinations in any order.
The same number may be chosen from the given array an unlimited number of times. Two combinations are unique if the frequency of at least one of the chosen numbers is different.
It is guaranteed that the number of unique combinations that sum up to target is less than 150 combinations for the given input.
Examples:
Input: candidates = [2,3,6,7], target = 7
Output: [[2,2,3],[7]]
Explanation: 2 and 3 are candidates, and 2 + 2 + 3 = 7. Note that 2 can be used multiple times. 7 is a candidate, and 7 = 7.
These are the only two combinations.
Input: candidates = [2,3,5], target = 8
Output: [[2,2,2,2],[2,3,3],[3,5]]
Input: candidates = [2], target = 1
Output: []
Explanation: No combinations are possible to generate as array as only 1 element i.e. 2
Constraints:
1 <= candidates.length <= 302 <= candidates[i] <= 40- All elements of
candidatesare distinct. 1 <= target <= 40
Solution
- Recursion (Take/NoTake Approach)
1. Recursion
Intuition
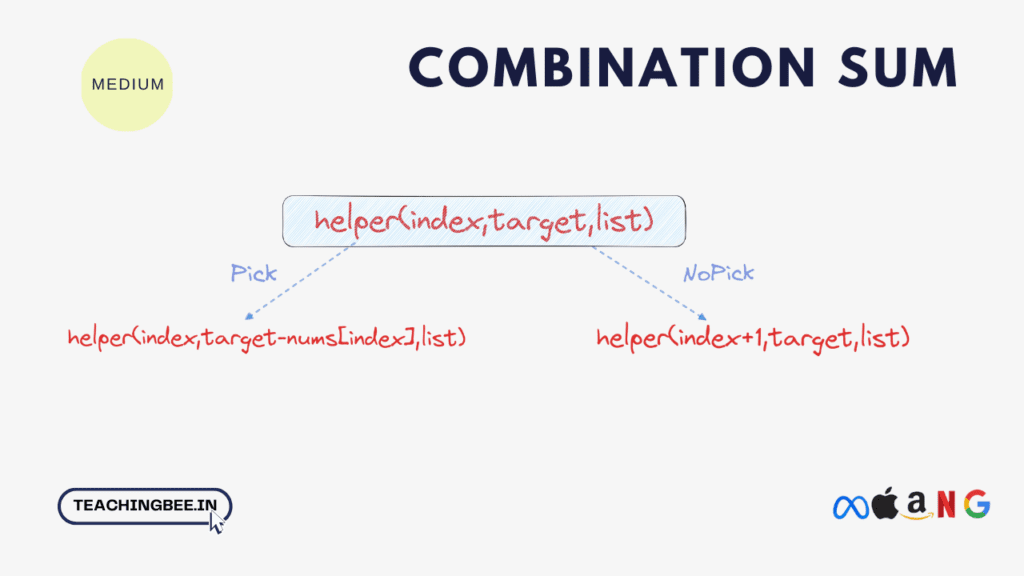
Whenever the question asks to find permutations or printing subsequences or something similar, think of recursion/backtracking. This problem uses the “pick and non-pick” approach. The idea is similar to subset sum problem.
Algorithm
We select each number from candidates array and recursively consider two possible cases:
- if(candidates[i]<target) then we have two cases:
- The selected number is part of the solution and included in the list.
- The selected number is not part of the solution and not included in the list.
- if(candidates[i]>target) then we have only 1 cases of not taking.


Base Case: There will be two base cases:
- if(target==0) it means we found the answer so the list that we were carrying in recursive function we will store in answer 2D list.
- if(index>=candidates.length) it means we haven’t found any possible answer so just return back.
Dry Run
We start with an empty data structure i.e. list in our case, the target value, and the index == 0. At each index, as discussed above there are two options:
- Include the element: Add the current element to the data structure. As duplicates are allowed, remain at the same index but reduce the target by the current element’s value.
- Exclude the element: Do not add the element and move on to the next index, keeping the target unchanged.
We recursively explore both options. When including an element, we make a recursive call at the same index after updating the target. The target value will be target-candidates[index] (if => candidates[i]<target). When excluding, the recursive call goes to the next index.
Before backtracking, we remove the element added in the previous call. This ensures we generate all permutations with and without the element at a given index.
The recursion terminates when the index>=candidates.length for a call or when target==0. The data structure then contains a valid combination summing to target.
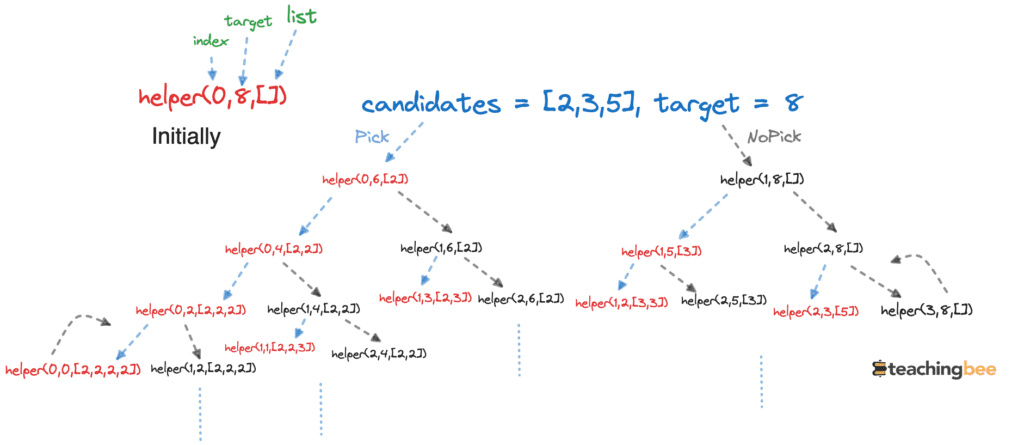

By recursively exploring all include/exclude choices at each index, we generate all possible combinations that sum up to the target. The backtracking and removal of elements ensures correct subsets.
Code Implementation
Here is the code implementation of combination sum in C++, Java, Python.
// Combination Sum C++ Solution
#include <vector>
#include <algorithm>
class Solution {
public:
void help(int index, std::vector<int>& nums, std::vector<int>& list, std::vector<std::vector<int>>& res, int target) {
// Answer found, store in res 2D vector.
if (target == 0) {
res.push_back(list);
return;
}
// No possible answer, return back.
if (index == nums.size()) return;
// Take call.
if (nums[index] <= target) {
list.push_back(nums[index]);
help(index, nums, list, res, target - nums[index]);
list.pop_back(); // Backtracking step.
}
// No take call.
help(index + 1, nums, list, res, target);
}
std::vector<std::vector<int>> combinationSum(std::vector<int>& candidates, int target) {
std::vector<std::vector<int>> res;
std::vector<int> list;
help(0, candidates, list, res, target);
return res;
}
};
// Combination Sum Java Solution
class Solution {
private void help(int index, int[] nums, List<Integer> list, List<List<Integer>> res, int target){
// Answer found store in res 2D list..
if(target==0){
res.add(new ArrayList<>(list));
return;
}
// No possible ans.. return back...
if(index==nums.length)
return;
// Take call...
if(nums[index]<=target) {
list.add(nums[index]);
help(index,nums,list,res,target-nums[index]);
list.remove(list.size()-1); // backtracking step...
}
// No take call...
help(index+1,nums,list,res,target);
}
public List<List<Integer>> combinationSum(int[] candidates, int target) {
List<List<Integer>> res= new ArrayList<>();
List<Integer> list = new ArrayList<>();
help(0,candidates,list,res,target);
return res;
}
}// Combination Sum Python Solution
class Solution:
def help(self, index, nums, list, res, target):
# Answer found, store in res list of lists.
if target == 0:
res.append(list[:])
return
# No possible answer, return back.
if index == len(nums):
return
# Take call.
if nums[index] <= target:
list.append(nums[index])
self.help(index, nums, list, res, target - nums[index])
list.pop() # Backtracking step.
# No take call.
self.help(index + 1, nums, list, res, target)
def combinationSum(self, candidates, target):
res = []
self.help(0, candidates, [], res, target)
return res
Complexity
Time Complexity: O(2^t * n) where t is the target, n is the average length
Space Complexity: O(n*x), n is the average length and x is the no. of combinations
I hope You liked the post ?. For more such posts, ? subscribe to our newsletter. Try out our free resume checker service where our Industry Experts will help you by providing resume score based on the key criteria that recruiters and hiring managers are looking for.