Table of Contents
ToggleBinary Search Tree in Data Structure (BST) are one of the most useful and versatile data structures in computer science. At its core, a BST is a hierarchical tree-based data structure that allows for efficient insertion, deletion and search operations. The properties that define a BST enable it to provide rapid access and modification to stored data based on key values.
In this comprehensive guide, we will cover what binary search tree are, the core properties that distinguish BST tree from ordinary binary trees, the common operations and traversals on BSTs, various types and variants of BSTs, their real-world applications, and some frequently asked questions.
Binary Search Tree In Data Structure
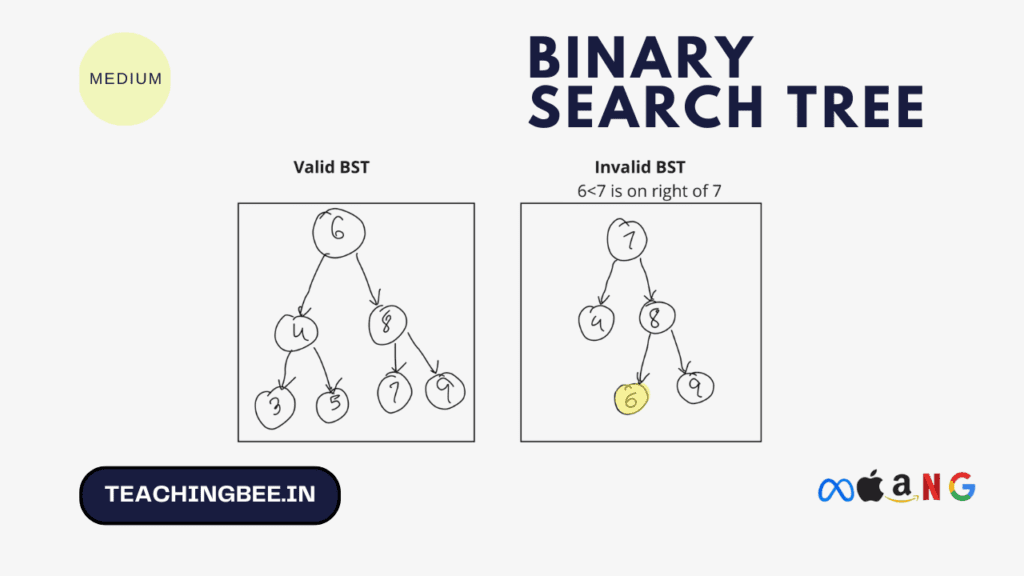
A Binary Search Tree (BST) is a tree data structure in which each node has at most two children, referred to as the left child and the right child that statisfies follwoing properties
Structure of BST:
- Root: The topmost node in a BST.
- Left Child: The child node that contains values less than the parent node.
- Right Child: The child node that contains values greater than the parent node.
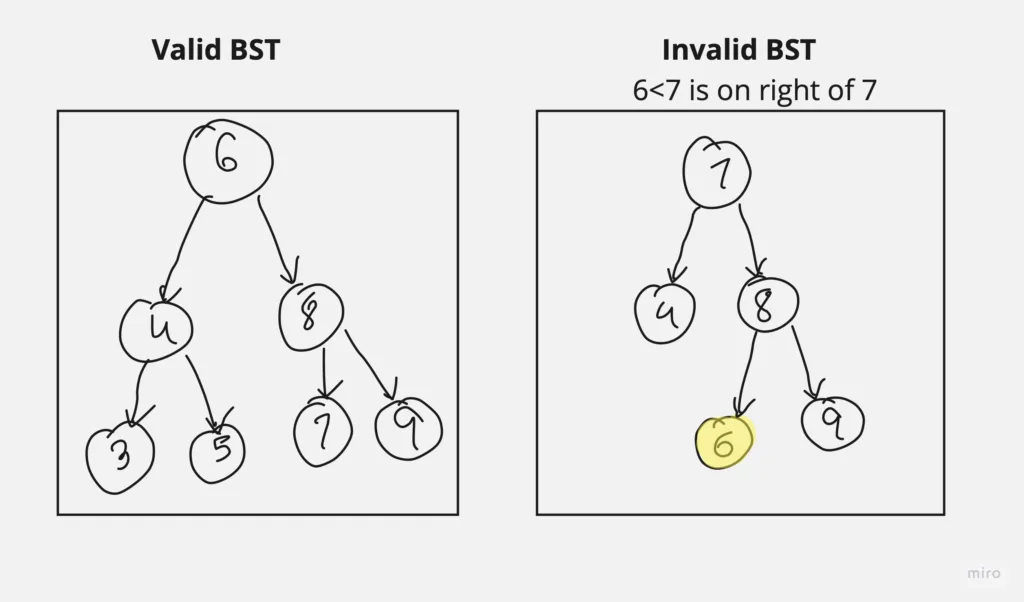

Properties of Binary Search Tree (BST)
The key properties of binary search trees (BST tree) are:
15
/ \
10 25
/ \ / \
5 12 20 271. Node’s left subtree contains smaller keys than node’s key
For any node, all keys in its left subtree are less than the node’s key. For example:
Here, 10, 5 and 12 are less than 15.
2. Node’s right subtree contains larger keys than node’s key
All keys in a node’s right subtree are greater than node’s key. For example:
25, 20 and 27 are greater than node 15.
3. Inorder traversal gives sorted keys
An inorder traversal visits left subtree, then root, then right subtree. This outputs keys in sorted order.
// Inorder traversal of BST
5 10 12 15 20 25 27 5. Left and right subtrees are also BSTs
Left and right subtrees under each node must follow BST properties recursively. This enables efficient search, insert, delete throughout the tree.
Types of BST
1. Full BST (Full Binary Search Tree) : A binary search tree where every node has zero or two children.
5
/ \
3 8
/ \
7 9 2. Complete BST (Complete Binary Search Tree) : A binary search tree where all levels are completely filled except possibly for the last level, which is filled from left to right.
5
/ \
3 8
/ \ /
1 4 73. Perfect BST (Perfect Binary Search Tree): A binary search tree where all levels are completely filled, and the number of nodes doubles as you move down the tree.
5
/ \
3 8
/ \ / \
1 4 7 9Note: Full BST Vs Perfect BST
A Perfect BST is perfectly balanced with a specific number of nodes, while a Full BST simply enforces that nodes have either zero or two children and may or may not be perfectly balanced.
A Perfect BST is characterized by its perfect balance and a specific number of nodes, while a Full BST enforces the presence of zero or two children per node but allows for more flexibility in terms of balance and node count.
4. Degenerate BST (Degenerate Binary Search Tree): A binary search tree where every node has only one child, essentially forming a linked list.
1
\
2
\
3
\
45. Balanced BST (Balanced Binary Search Tree): A binary search tree where the height is logarithmic in the number of nodes, ensuring efficient operations. It may not always be perfectly balanced but maintains reasonable balance.
5
/ \
3 8
/ \ \
1 4 9Binary Search Tree in Data Structure Implementation And Operations
Let’s discuss major binary search tree implementation and various operations supported that are:
- Insertion
- Deletion
- Search
Binary Search Tree Insertion
Binary Search Tree Insertion involves adding a new element while maintaining the BST property, which ensures that elements to the left of a node are smaller, and elements to the right are larger. There are different cases to consider during insertion to ensure the tree remains a valid BST. Here are some common cases:
- Insertion into an Empty Tree:
- If the tree is initially empty, simply create a new node as the root.
- Insertion into a Non-Empty Tree:
- Start at the root and traverse the tree by comparing the value to be inserted with the values of nodes.
- Move to the left subtree if the value is less than the current node’s value or to the right subtree if it’s greater.
- Continue this process until you find an empty spot (i.e., a null pointer) and insert the new node there.
- Insertion of a Duplicate Value:
- Depending on your implementation, you can either allow duplicates (insert them as separate nodes) or handle them differently (e.g., by incrementing a counter in the node).
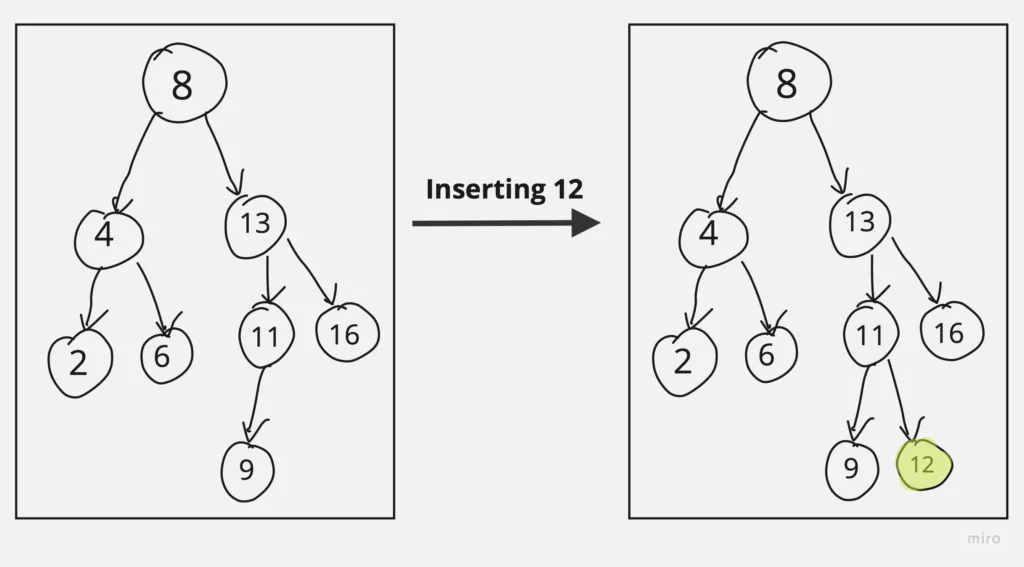

Now, let’s see code of insertion in binary search tree in Java and C++:
C++
// BST Implementation In C++ : Insertion
#include <iostream>
// Define the structure of a BST node
struct Node {
int data;
Node* left;
Node* right;
Node(int value) : data(value), left(nullptr), right(nullptr) {}
};
// Function to insert a value into a BST
Node* insert(Node* root, int value) {
// If the tree is empty, create a new node as the root
if (root == nullptr) {
return new Node(value);
}
// Traverse the tree to find the appropriate position for insertion
if (value < root->data) {
root->left = insert(root->left, value); // Recursively insert into the left subtree
} else if (value > root->data) {
root->right = insert(root->right, value); // Recursively insert into the right subtree
}
return root; // Return the updated root
}
int main() {
Node* root = nullptr; // Initialize an empty tree
// Insert nodes into the BST
root = insert(root, 5);
root = insert(root, 3);
root = insert(root, 8);
root = insert(root, 1);
root = insert(root, 4);
// Perform any necessary operations with the BST
// (e.g., inorder traversal to check the result)
return 0;
}
Java
// BST Implementation In Java : Insertion
class Node {
int data;
Node left, right;
public Node(int value) {
data = value;
left = right = null;
}
}
public class BST {
Node root;
// Constructor to initialize an empty tree
public BST() {
root = null;
}
// Function to insert a value into the BST
public Node insert(Node root, int value) {
// If the tree is empty, create a new node as the root
if (root == null) {
root = new Node(value);
return root;
}
// Traverse the tree to find the appropriate position for insertion
if (value < root.data) {
root.left = insert(root.left, value); // Recursively insert into the left subtree
} else if (value > root.data) {
root.right = insert(root.right, value); // Recursively insert into the right subtree
}
return root; // Return the updated root
}
public static void main(String[] args) {
BST bst = new BST();
// Insert nodes into the BST
bst.root = bst.insert(bst.root, 5);
bst.root = bst.insert(bst.root, 3);
bst.root = bst.insert(bst.root, 8);
bst.root = bst.insert(bst.root, 1);
bst.root = bst.insert(bst.root, 4);
// Perform any necessary operations with the BST
// (e.g., inorder traversal to check the result)
}
}Binary Search Tree Deletion
Binary Search Tree Deletion involves several cases to consider to maintain the BST’s properties. The key idea is to replace the node to be deleted with either its in-order predecessor or in-order successor, if they exist, or handle the deletion differently based on the node’s children. Here are the various cases for deletion:
- Node with No Children (Leaf Node):
- Simply remove the node from the tree.
- Node with One Child:
- Replace the node with its child.
- Node with Two Children:
- Find either the in-order predecessor or in-order successor.
- Copy the value of the predecessor/successor to the node to be deleted.
- Delete the predecessor/successor node.
- Deletion of the Root Node:
- Special case when the root node is to be deleted.
- Replace the root node with its in-order predecessor or successor (based on preference).
- Delete the predecessor/successor node as needed.
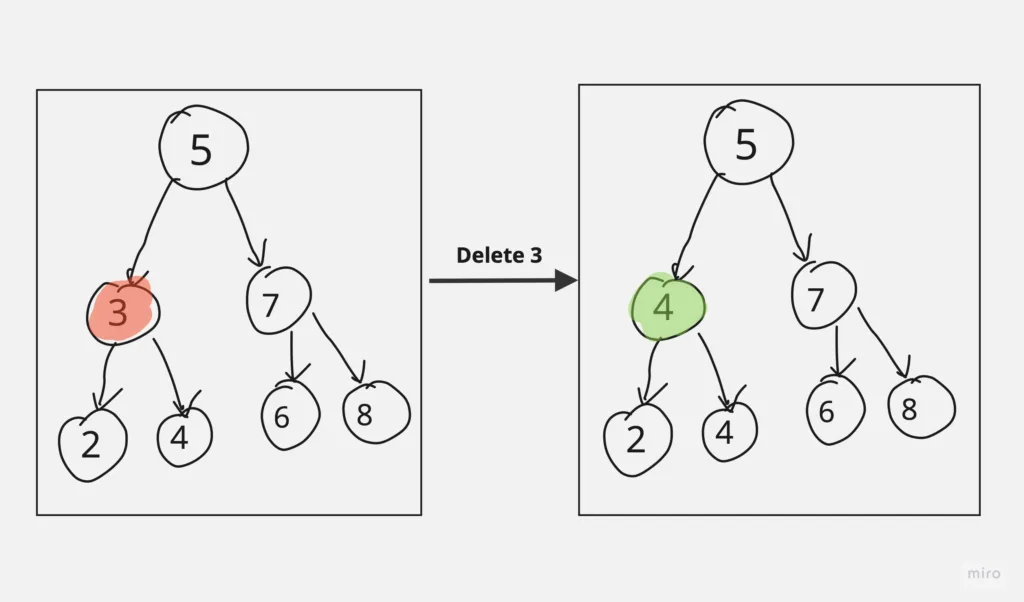

Let’s see binary search tree implementation for deleting a node in binary search tree in Java and C++:
C++
// BST Implementation In C++ : Deletion
#include <iostream>
// Define the structure of a BST node
struct Node {
int data;
Node* left;
Node* right;
Node(int value) : data(value), left(nullptr), right(nullptr) {}
};
// Function to find the in-order predecessor (maximum value in the left subtree)
Node* findMax(Node* node) {
while (node->right != nullptr) {
node = node->right;
}
return node;
}
// Function to delete a node with a given value from the BST
Node* deleteNode(Node* root, int value) {
if (root == nullptr) {
return root; // Node not found
}
// Traverse the tree to find the node to delete
if (value < root->data) {
root->left = deleteNode(root->left, value);
} else if (value > root->data) {
root->right = deleteNode(root->right, value);
} else {
// Node to be deleted found
// Case 1: Node with only one child or no child
if (root->left == nullptr) {
Node* temp = root->right;
delete root;
return temp;
} else if (root->right == nullptr) {
Node* temp = root->left;
delete root;
return temp;
}
// Case 2: Node with two children, find in-order successor (or predecessor)
Node* temp = findMax(root->left); // In-order predecessor
root->data = temp->data;
root->left = deleteNode(root->left, temp->data);
}
return root;
}
int main() {
Node* root = nullptr; // Initialize the BST
// Insert nodes into the BST
// (Insertion code goes here)
// Delete a node from the BST
// root = deleteNode(root, value);
// Perform any necessary operations with the modified BST
// (e.g., inorder traversal to check the result)
return 0;
}Java
// BST Implementation In Java : Deletion
class Node {
int data;
Node left, right;
public Node(int value) {
data = value;
left = right = null;
}
}
public class BST {
Node root;
public BST() {
root = null;
}
// Function to find the in-order predecessor (maximum value in the left subtree)
private Node findMax(Node node) {
while (node.right != null) {
node = node.right;
}
return node;
}
// Function to delete a node with a given value from the BST
public Node deleteNode(Node root, int value) {
if (root == null) {
return root; // Node not found
}
// Traverse the tree to find the node to delete
if (value < root.data) {
root.left = deleteNode(root.left, value);
} else if (value > root.data) {
root.right = deleteNode(root.right, value);
} else {
// Node to be deleted found
// Case 1: Node with only one child or no child
if (root.left == null) {
Node temp = root.right;
return temp;
} else if (root.right == null) {
Node temp = root.left;
return temp;
}
// Case 2: Node with two children, find in-order successor (or predecessor)
Node temp = findMax(root.left); // In-order predecessor
root.data = temp.data;
root.left = deleteNode(root.left, temp.data);
}
return root;
}
public static void main(String[] args) {
BST bst = new BST();
// Insert nodes into the BST
// (Insertion code goes here)
// Delete a node from the BST
// bst.root = bst.deleteNode(bst.root, value);
// Perform any necessary operations with the modified BST
// (e.g., inorder traversal to check the result)
}
}
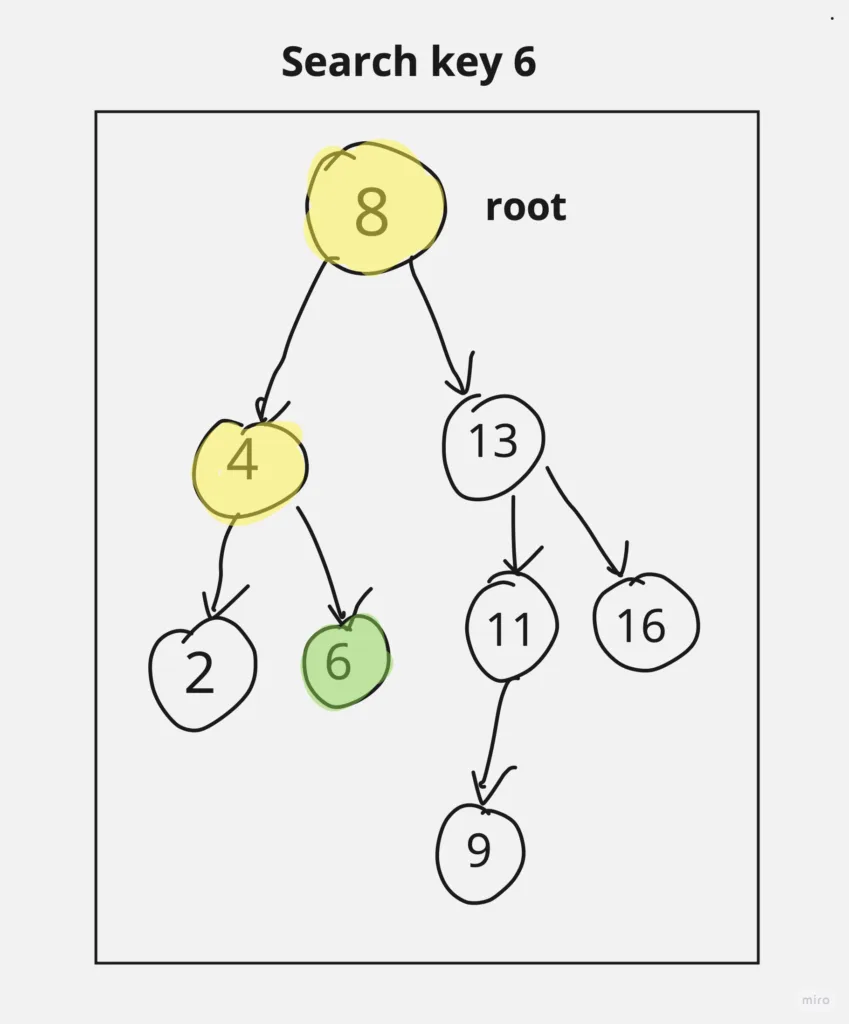
Binary Search Tree Search
Searching in a Binary Search Tree (BST) involves traversing the tree to find a specific value efficiently. There are three common cases to consider when searching for a value in a BST:
- Value Found: The value you are searching for is found in the current node, and you can return the node or perform the desired action.
- Value Less than Current Node: If the value you are searching for is less than the current node’s value, continue the search in the left subtree.
- Value Greater than Current Node: If the value you are searching for is greater than the current node’s value, continue the search in the right subtree.

C++
// BST Implementation In C++ : Searching
#include <iostream>
// Define the structure of a BST node
struct Node {
int data;
Node* left;
Node* right;
Node(int value) : data(value), left(nullptr), right(nullptr) {}
};
// Function to search for a value in the BST
Node* search(Node* root, int value) {
// If the tree is empty or the value is found
if (root == nullptr || root->data == value) {
return root;
}
// If the value is less than the current node's value, search in the left subtree
if (value < root->data) {
return search(root->left, value);
}
// If the value is greater than the current node's value, search in the right subtree
return search(root->right, value);
}
int main() {
Node* root = nullptr; // Initialize the BST
// Insert nodes into the BST
// (Insertion code goes here)
int targetValue = 42; // Value to search for
Node* result = search(root, targetValue);
if (result != nullptr) {
std::cout << "Value " << targetValue << " found in the BST." << std::endl;
} else {
std::cout << "Value " << targetValue << " not found in the BST." << std::endl;
}
return 0;
}
Java
// BST Implementation In Java : Searching
class Node {
int data;
Node left, right;
public Node(int value) {
data = value;
left = right = null;
}
}
public class BST {
Node root;
// Function to search for a value in the BST
public Node search(Node root, int value) {
// If the tree is empty or the value is found
if (root == null || root.data == value) {
return root;
}
// If the value is less than the current node's value, search in the left subtree
if (value < root.data) {
return search(root.left, value);
}
// If the value is greater than the current node's value, search in the right subtree
return search(root.right, value);
}
public static void main(String[] args) {
BST bst = new BST();
// Insert nodes into the BST
// (Insertion code goes here)
int targetValue = 42; // Value to search for
Node result = bst.search(bst.root, targetValue);
if (result != null) {
System.out.println("Value " + targetValue + " found in the BST.");
} else {
System.out.println("Value " + targetValue + " not found in the BST.");
}
}
}Real World Applications of Binary Search Tree (BST)
| Use Case | Description |
|---|---|
| Phonebook | Storing and searching for contacts based on names, where names are ordered alphabetically. |
| File System Indexing | Organizing file systems hierarchically and quickly searching for files by name or path. |
| Library Catalog | Managing a library’s collection of books, sorted by title, author, or publication date. |
| Auto-Complete | Implementing auto-complete suggestions for search engines and text editors based on words. |
| Stock Price Tracking | Storing and searching for historical stock prices, allowing quick retrieval by date. |
| Dictionary | Building a dictionary to look up word definitions efficiently, sorted alphabetically. |
| Employee Hierarchy | Representing an organization’s hierarchy with employees, making it easy to find managers. |
| Network Routing | Routing data packets efficiently in computer networks by comparing IP addresses. |
| Database Indexing | Indexing databases for fast retrieval of records based on indexed columns (e.g., IDs). |
| Genetic Trees | Representing and analyzing evolutionary relationships among species in biology. |
Try out our free resume checker service where our Industry Experts will help you by providing resume score based on the key criteria that recruiters and hiring managers are looking for.
Checkout how to print left view of binary tree in this great article
FAQ On Binary Search Tree (BST)
What is difference Between binary tree and binary search tree?
A binary tree is a general hierarchical structure with nodes having at most two children, while a binary search tree (BST) enforces an ordering rule where left subtree values are less than the node’s value, and right subtree values are greater, making it efficient for searching and sorting operations.
How does a binary search tree work ?
A Binary Search Tree (BST) is a data structure that organizes elements in a tree-like structure where each node has atmost two children and values to the left are smaller, and values to the right are larger, making it efficient for searching, insertion, and deletion operations.
This allows for efficient log(n) time complexity for search, insert, and delete operations on average, where ‘n’ is the number of elements in the tree.
Can a Binary Search Tree not be perfect while fulfilling the perfect BST requirements?
Yes, a Binary Search Tree (BST) can fulfill the requirements of a perfect BST in terms of structure (i.e., having zero or two children for each node) but still not be considered a “perfect” BST in a broader sense.
A “perfect” BST typically refers to a tree where all levels are completely filled, and the number of nodes doubles as you move down the tree. In such a tree, the height is precisely balanced, ensuring optimal search and insertion times. It has 2^h – 1 nodes at level ‘h’, where ‘h’ is the height of the tree.
However, even if a BST has the structural characteristics of a perfect BST (every node has zero or two children), it might not have the specific node count that would make it a “perfect” BST. It could have fewer nodes, and its height might not be balanced to the same extent as a true perfect BST.
What are the differences between BST and balanced BST?
Balanced BSTs like AVL and Red-Black trees do extra balancing steps on insertion/deletion to ensure tree height is reduced. This results in faster searches. Simple BSTs can become skewed and unbalanced over time.
What are the different BST traversal techniques?
The main traversals are: inorder (left-root-right), preorder (root-left-right), postorder (left-right-root). Inorder gives sorted key sequence, preorder helps reconstruct tree, postorder used to delete tree nodes.