Table of Contents
ToggleIn the world of computer science there are many applications of linked lists. Linked lists are among the fundamental data structures in computer science. They provide an efficient and flexible way to store sequenced data. Unlike arrays, linked lists consist of non-contiguous memory allocations tied together by pointers. This dynamic structure allows easy insertion and removal of elements. There are many applications of Linked lists in real life and it also find widespread use across many algorithms.
In this article, we will explore some of the key applications of linked lists that highlight their utility as an indispensable data structure.
What Are Linked Lists?
The linked list can be described as a data structure that consists of a collection of nodes, where each node connects to the next one with the help of pointer. Pointer is an object in many programming languages that stores a memory address.
Every node is made up of data as well as an index to the next node. The general design of Linked List is as follows:
struct node
{
// Singly Linked List Structure
int data;
struct node *next;
};A linked list may be large or small. No matter its size, the components which make up it are nothing more than nodes. The linked lists are simply an array of nodes.


As you can see in the picture above, the point of entry in the listing is the first node. This is known by the name of head. The final node on the list is usually called its tail. The last node of the list isn’t actually a node, but a symbol which points to the empty or null value.
Types Of Linked List
There are majorly three types of LinkedList:
- Singly Linked List
- Doubly Linked List
- Circular Linked List
Singly Linked List
As illustrated in the following image, the lists are singly linked. They include nodes with information and a pointer that indicates another node.Singly linked list only has forward pointer and last node points to NULL.
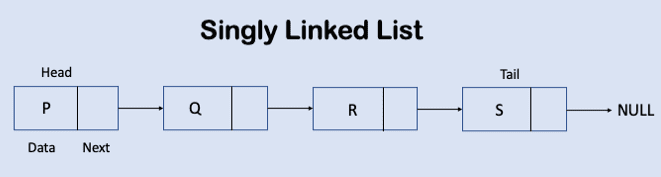

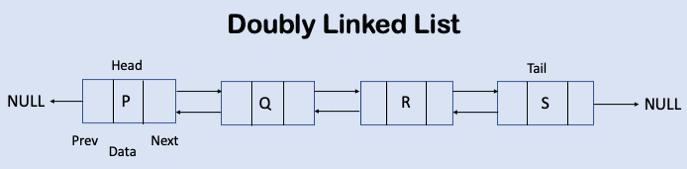
Doubly Linked List
A doubly linked list contains nodes with 3 fields, namely a value, a forward reference towards the following node and a return reference to the prior node.

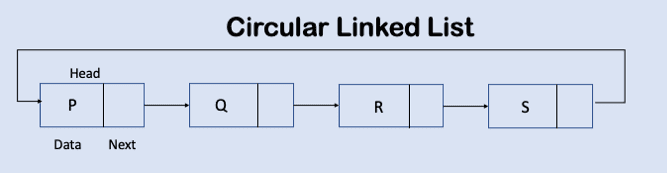
Circular Linked List
Circular linked lists can be compared to a single linked list, however the differentiator lies in the last node of the list , the tail node is pointing towards the node that is at its head. The benefit lies in the ability to traverse the entire list beginning at any point.

Complexity
| Data structure | Access | Search | Insertion | Deletion |
| Singly Linked list | O(N) | O(N) | O(1) | O(1) |
| Doubly Linked List | O(N) | O(N) | O(1) | O(1) |
| Circular Linked List | O(N) | O(N) | O(1) | O(1) |
Let’s now look into some of the applications of linked lists in data structure.
Applications of Linked Lists
Some of the Applications Of Linked Lists are:
- Symbol Table Creation in Compilers
- Task Scheduling in Operating Systems
- Image Viewer Navigation
- Efficient Directory Management
- Long Integer Arithmetic
- Polynomial Manipulation
- Undo/Redo Functionality in Software
- Efficient Sparse Matrix Representation
- Dynamic Memory Allocation
- Robotics Control Systems
- Adjacency List Representation Of Graphs
Let’s look some of these in detail.
Symbol Table Creation in Compilers
A symbol table is a data structure used by compilers to store information about identifiers (variables, functions, etc.) in a program. It maps the names of identifiers to their attributes, such as data type, scope, and memory location. Linked lists can be employed in symbol table creation for efficient management of identifiers.
Example:
Consider the following C code snippet:
int main() {
int x = 5;
float y = 2.5;
return 0;
}In this case, the symbol table may have entries like:
| Identifier | Data Type | Scope | Memory Location |
|---|---|---|---|
| main | int | global | 0x00400500 |
| x | int | local | 0x7fff5fbff7e4 |
| y | float | local | 0x7fff5fbff7e0 |
Each entry is stored as a node in a linked list, allowing for efficient insertion, retrieval, and modification of symbol information during the compilation process.
Task Scheduling in Operating Systems
Task scheduling is a crucial aspect of operating systems that involves determining the order in which processes are executed by the CPU. Linked lists are commonly used to manage the queue of processes waiting to be executed. Each process is represented as a node in the linked list, and the operating system can traverse the list to determine the next process to execute.
Example:
Consider a simple operating system with three processes: A, B, and C. The ready queue, implemented as a linked list, may look like this:
[A] -> [B] -> [C]If the operating system follows a round-robin scheduling algorithm, it will execute each process in turn, cycling through the linked list. After executing process A, the list becomes:
[B] -> [C] -> [A]This continues, ensuring fair execution of processes.
Long Integer Arithmetic
Long integer arithmetic involves performing arithmetic operations on integers that exceed the size of native data types. Linked lists can be used to represent and manipulate long integers by breaking them down into manageable chunks.
Example:
Consider the addition of two long integers:
6789012345
+ 4321012345
-------------------
11120014690In this case, each digit is stored in a node of a linked list, and the addition operation is performed by traversing the linked lists from the least significant digit (at the tail of the list) to the most significant digit (at the head of the list).
6 -> 7 -> 8 -> 9 -> 0 -> 1 -> 2 -> 3 -> 4 -> 5
+ 4 -> 3 -> 2 -> 1 -> 0 -> 1 -> 2 -> 3 -> 4 -> 5
-----------------------------------------------
1 -> 1 -> 1 -> 2 -> 0 -> 0 -> 1 -> 4 -> 6 -> 9 -> 0
Image Viewer Navigation
Image viewers employ linked lists to navigate through a series of images. Each image is a node, and the linked list enables seamless movement between images, providing a flexible and intuitive viewing experience. Users can easily traverse forward or backward through the linked images, creating a smooth and interactive navigation system.
Efficient Directory Management
In directory management, linked lists are utilized to represent the hierarchical structure of directories. Each directory is a node, connected to its parent and child directories, streamlining operations like creation, deletion, and navigation. This hierarchical organization facilitates efficient management of files and directories in a computer system.
Polynomial Manipulation
Linked lists are employed in polynomial manipulation to represent the terms of a polynomial. Each term is a node, storing the coefficient and exponent of a polynomial element. This linked list structure facilitates the addition, subtraction, and multiplication of polynomials by traversing and manipulating the polynomial terms efficiently.
Example
Let’s consider a polynomial: 3x2+5x+2.
The linked list representation can be visualised as follows:
Node 1 Node 2 Node 3
+------+ +------+ +------+
| coef | 3 | coef | 5 | coef | 2
|------+ |------+ |------+
| exp | 2 | exp | 1 | exp | 0
|------+ |------+ |------+
| next | ----------> | next | ----------> | next | NULL
+------+ +------+ +------+In this representation:
- Each node represents a term in the polynomial.
- The “coef” field stores the coefficient of the term.
- The “exp” field stores the exponent of the term.
- The “next” field points to the next term in the polynomial. The last node has a “next” field pointing to NULL, indicating the end of the polynomial.
This linked list structure allows for efficient representation and manipulation of polynomials. Adding or removing terms involves updating the links between nodes, and traversing the list allows for operations like polynomial addition, subtraction, and multiplication.
Undo/Redo Functionality in Software
Software applications implement undo/redo functionality using linked lists, where each action that can be undone or redone is represented as a node in a doubly linked list. This structure allows users to navigate through a sequence of actions and revert or reapply changes, enhancing user control and editing capabilities.
Efficient Sparse Matrix Representation
Sparse matrices, which contain mostly zero elements, are efficiently represented using linked lists. Each non-zero element is a node, storing its row, column, and value. This representation optimizes memory usage and facilitates operations on sparse matrices by selectively traversing only the non-zero elements.
Example:
Consider the sparse matrix:
[ 0 0 3 0 0 ]
[ 0 7 0 8 0 ]
[ 0 0 0 0 0 ]
[ 0 0 5 0 0 ]The linked list representation could look like this:


In this representation:
- Each row in the matrix corresponds to a linked list.
- Each node in the linked list represents a non-zero element in the matrix.
- The “col” field stores the column index of the non-zero element.
- The actual value of the non-zero element is not explicitly stored (assumed to be non-zero).
- The “next” field points to the next non-zero element in the row.
This linked list structure efficiently represents sparse matrices by only storing information about non-zero elements, saving memory compared to dense matrix representations. The traversal of these lists facilitates matrix operations like addition, multiplication, and transpose.
Dynamic Memory Allocation
Linked lists play a key role in dynamic memory allocation, allowing for the efficient management of free memory blocks. The linked list maintains a sequence of free memory blocks, and when memory allocation is required, nodes are allocated and linked, ensuring effective utilization and organization of memory resources.
Robotics Control Systems
In robotics control systems, linked lists are used to implement control algorithms and sequences of robotic actions. Each action or state is represented as a node, and the linked list structure enables the robot to traverse through a predefined sequence, facilitating precise and programmable control of robotic movements and tasks.
Adjacency List Representation Of Graphs
Graphs are commonly represented using linked lists in the form of adjacency lists. Each vertex of the graph is a node, and its adjacent vertices are linked, forming an adjacency list. This representation is efficient for sparse graphs and allows for quick retrieval of neighboring vertices, making it widely used in graph-related algorithms and applications.
Real Life Applications Of Linked List
Music Playlist Management
Linked lists are widely used in music playlist management applications. Each song in the playlist is represented as a node, linked to the next song. This structure allows for easy insertion, deletion, and traversal of the playlist, providing a seamless music listening experience.
Train Reservation Systems
Train reservation systems utilize linked lists to manage seat bookings. Each seat is represented as a node, linked to the next available seat. This allows for efficient booking and cancellation of seats, optimizing the utilization of train resources.
Browser History in Web Browsers
Web browsers maintain a history of visited web pages using linked lists. Each webpage is a node, connected to the previously visited and next pages. Linked lists enable users to navigate back and forth through their browsing history with ease.
Photo Gallery
In photo gallery applications, linked lists can be utilised to manage and navigate through a collection of images. Each image is a node, connected to the next image, enabling users to easily move forward and backward through their image gallery.
Mailing List Management
Email systems often use linked lists to handle mailing lists efficiently. Each email address is represented as a node, linked to the next address. This structure allows for easy management of subscriber lists, including additions, removals, and updates.
Applications Of Singly Linked List
- Stack implementation – Singly linked lists allow efficient push and pop operations from only one end (top of stack), making them useful for implementing stacks.
- Queue implementation – Adding elements at the tail and removing from the head in a singly linked list makes it behave like a queue data structure.
- Dynamic memory allocation – The one way growth of singly linked lists enables allocating memory blocks dynamically as needed without upfront memory reservation.
- Hash table chaining – Hash collisions are handled by chaining elements hashing to the same slot using singly linked lists. Supports efficient insertion and deletion.
- Web browser history – Browsers use singly linked lists to efficiently maintain linear history of web pages visited by the user, allowing traversal back and forth using prev and next pointers.
- Caches with LRU replacement – Caches use an ordering policy like LRU to discard least recently used elements. Singly linked lists allow cheap insertions/deletions from both ends crucial for this.
Applications Of Doubly Linked List
- Recently Opened Files Management – Bidirectional links ease navigation through recently opened files, allowing efficient traversal in both forward and backward directions.
- Shopping Cart Operations – Insertions and deletions are streamlined in user shopping carts and wish-lists, leveraging the flexibility of doubly linked lists.
- Multi-level Undo in Editors – Sophisticated editors implement multi-level undo functionality through doubly linked list stacks, preserving the history of operations for undo/redo.
- Tabbed Interface Navigation– Bidirectional traversal facilitates seamless toggling between document interface tabs, enhancing user experience in tabbed interfaces.
- Photo Tagging Efficiency – Efficiently manage photo tagging, leveraging the benefits of cheap insertions/deletions and bidirectional traversal in doubly linked lists.
- LRU Caching Optimisation – Implement LRU caching with doubly linked lists for efficient removal of least recently used elements, crucial for page replacement policies.
Applications Of Circular Linked List
- Round Robin Scheduling Mechanism – Circular linked lists provide a queue-like FIFO mechanism, crucial for implementing round-robin scheduling in operating systems.
- Image Slideshow Carousel – Display images in an infinitely rotating carousel order, facilitated by circular linkage in a circular linked list.
- Music Shuffle Playback – Enable seamless music playback with repeat/shuffle options, leveraging cyclic pointers in circular linked lists.
- Round Table Discussion Tracking – Facilitate circular meeting formats by tracking discussion points efficiently using circular linked lists.
- Conveyor Mechanism Modelling – Model the movement of products on conveyor belts by utilizing the circular motion of links in circular linked lists.
- Traffic Management Optimisation – Improve vehicular traffic flow around circular pathways, such as road intersections, through efficient circular linked list management.
Conclusion
In this article we discussed various applications of linked lists. Lists are among the most well-known and efficient data structures that can be implemented in every programming language , including C, C++, Python, Java, and C#.
Additionally linked lists can be an excellent way to understand how pointers function. When you practice manipulating linked lists, it is possible to make yourself ready for more sophisticated data structures such as trees and graphs.
Checkout more Data Structure Tutorials here.
Try out our free resume checker service where our Industry Experts will help you by providing resume score based on the key criteria that recruiters and hiring managers are looking for.


