C Program To Find Product Of Two Numbers Using Recursion

In this blog post, we will see how to write C Program to Find Product of Two Numbers using Recursion with detailed explanation.

Before we start let’s understand few basic.

Multiplication can be seen as repeated addition. The product of two numbers let’s say num1* num2 can be seen addition of num1 to itself num2 times.

Example: Let’s take the number 3 and 5

3*5= 3+3+3+3+3 =15

We will use this concept to write are recursive relation.

Recursive Relation

f(n1,n2)= n1+ f(n1, n2-1)

To write a C Program to Find Product of Two Numbers using Recursion you can follow this algorithm and corresponding pseudo code.

Algorithm:

1. Input:
   • Take two numbers as input, let’s call them num1 and num2.
2. Base Case Check:
   • Check if either of the numbers is zero. If so, return 0 because any number multiplied by zero is zero. This is the stopping point for our calculation.
3. Recursive Case:
   • If neither of the numbers is zero, perform the following steps:
     • Take num1 and add it to the result of a recursive call with the same num1 and num2 decreased by 1.
     • This step essentially means adding num1 to itself num2 times.
4. Repeat:
   • Repeat the recursive case until the base case is met. In each step, we add num1 to the result, effectively simulating multiplication.
5. Output:
   • The final result obtained after the recursion represents the product of the two input numbers.

C Program To Find Product Of Two Numbers Using Recursion

#include <stdio.h>

// Function to find the product of two numbers using recursion
int findProduct(int num1, int num2) {
    // Base Case
    if (num1 == 0 || num2 == 0) {
        return 0;
    }

    // Recursive Case
    return num1 + findProduct(num1, num2 - 1);
}

int main() {
    // Example Numbers
    int number1 = 5;
    int number2 = 3;

    // Find and print the product
    int result = findProduct(number1, number2);
    printf("Product of %d and %d: %d\n", number1, number2, result);

    return 0;
}

Output

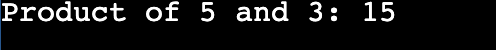
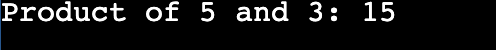
In the above program,

• The findProduct function takes two integers num1 and num2 as input and multiples it using recursion.
• In the base case, if either of num is 0, the recursion returns 0 for that case.
• In the recursive case, it adds the num1 and function call itslf with decremented value of num2.
• Finally, the sum is returned.

The execution flow for the input values 2 and 5 would unfold as follows:

1. Initial call: findProduct(3, 5)
   • Recursive call 1: findProduct(3, 4)
     • Recursive call 2: findProduct(3, 3)
       • Recursive call 3: findProduct(3, 2)
         • Recursive call 4: findProduct(3, 1)
           • Recursive call 5: findProduct(3, 0)
             • Base Case: Return 0
           • Result from Recursive call 5: 0
         • Result from Recursive call 4: 3 + 0 = 3
       • Result from Recursive call 3: 3 + 3 = 6
     • Result from Recursive call 2: 3 + 6 = 9
   • Result from Recursive call 1: 3 + 9 = 12
   • Result from Recursive Initial Call: 3+12=15
2. Final result: 15

Therefore, the product of 3 and 5 is 15, as demonstrated by the recursion in the C program.

If you liked this post you can checkout other C Programs.

FAQ

How is multiplication achieved through recursion in this function?

Multiplication is achieved through repeated addition. The recursive case includes the expression return num1 + findProduct(num1, num2 - 1), where the function calls itself with the same num1 and decrements num2 by 1 in each recursion. This process continues until the base case is met, effectively summing num1 repeatedly.

How can I modify the function to handle negative numbers correctly?

To handle negative numbers, you should consider adjusting the base case or implementing additional checks. One approach is to modify the base case to check for both num1 and num2 being zero or handle negative numbers separately. It’s important to define the desired behavior for negative inputs based on the specific requirements of the program.