Ultimate Guide For Cohen Sutherland Line Clipping Algorithm

The process of cutting the part of line lying outside the view pane is called line clipping. The following algorithms are used for line clipping:

• Cohen Sutherland Line Clipping Algorithm
• Liang-Barsky Line Clipping Algorithm
• Midpoint Subdivision Line Clipping Algorithm

In this article we will focus on Cohen Sutherland Line Clipping Algorithm and its implementation

Viewport

The viewport is a region of the window in which graphics are displayed.

Problem Statement

Cohen Sutherland Line Clipping Algorithm

In Cohen Sutherland Line Clipping Algorithm the viewing space is divided into nine encoded regions. For each endpoint of a line segment, we assign a 4-bit code following the rules below

• bit 1 is 1 if x<X_min
• bit 2 is 1 if x>X_max
• bit 3 is 1 if y< Y_min
• bit4 is1 if y>Y_max

So, based on above rule the regions with code will look like below

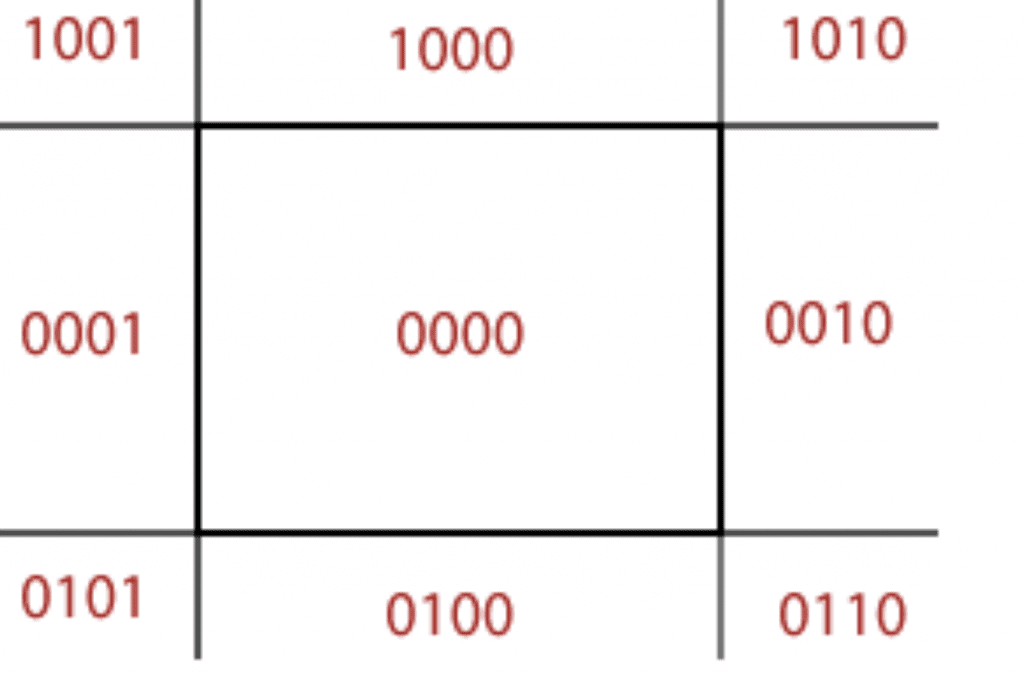
For any line in Cohen Sutherland Line Clipping Algorithm there are three cases possible

1. Completely Within the View Port : IF Bitwise OR of region code of two end points of line is 0, as both endpoints will have region code as 0000.
2. Completely outside the View Port : Both endpoints share at least one outside region which implies that the line does not cross the visible region. (bitwise AND of endpoints != 0).
3. Partially inside the window : Both endpoints are in different regions. In this case, the algorithm finds one of the two points that is outside the rectangular region. The intersection of the line from outside point and rectangular window becomes new corner point and the algorithm repeats

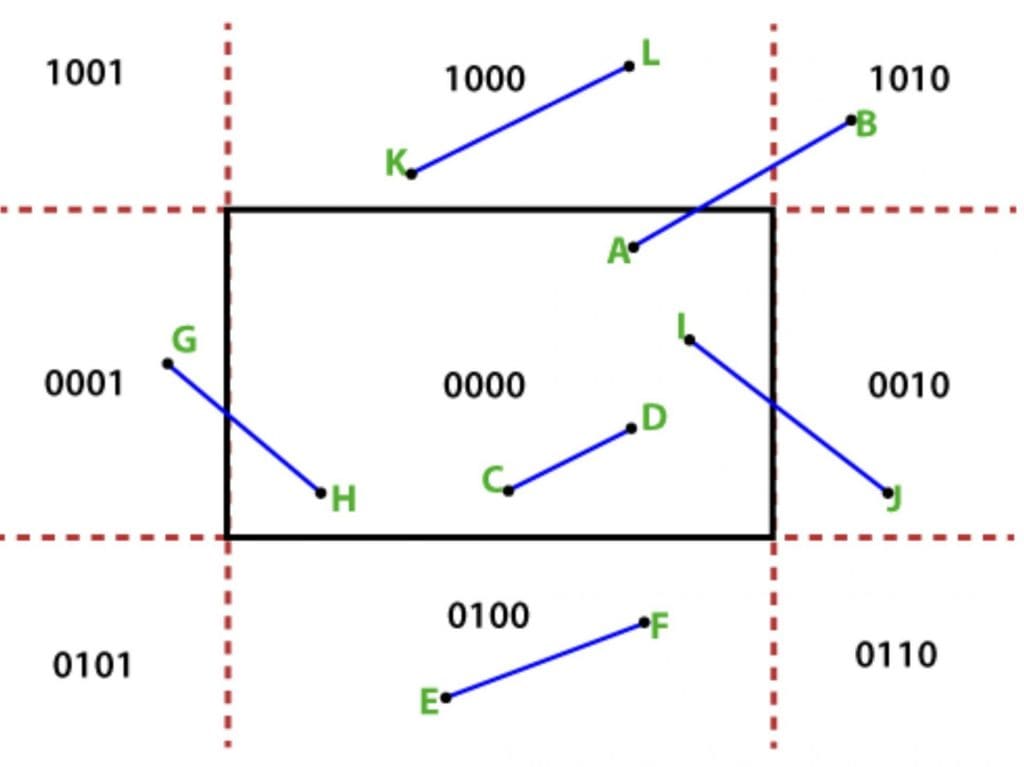
• From above figure we can see line KL is completely outside the RegionCode(K) AND RegionCode(L) !=0
• Similarly Line CD. is completely inside and OR of its region code of endpoints is 0
• For the obvious reasons line GH needs to be clipped.

Let’s look at Pseudocode for Cohen Sutherland Line Clipping Algorithm

1. Assign a region code for two endpoints of given line.
2. Perform OR operation on both endpoints of the line.
      IF Result of OR is 0 
         Then Line is completely within viewport 
      ELSE
         Perform And Operation on both endpoints
         IF Result of And is not 0
            Then given line is completely outside
         ELSE
            Clip the line
            a. Find intersection points with boundaries using:  
               m = (y1-y0) (x1-x0)
            b. When the line intersects:
               Left side boundary of the window port: x = Xmin
               Right side boundary of the window port: x = Xmax
               Top side boundary of the window port: y = Ymax
               Bottom side boundary of the window port: y= Ymin
3. Repeat step 2 until we find a clipped line either trivially accepted or trivially rejected.
4. Repeat step 1 for other lines

Implementation

// C++ program to implement Cohen Sutherland Line Clipping Algorithm

#include <iostream>
using namespace std;

// Assigning codes to region
const int INSIDE = 0; // 0000
const int LEFT = 1; // 0001
const int RIGHT = 2; // 0010
const int BOTTOM = 4; // 0100
const int TOP = 8; // 1000

// Defining view port coordinates
const int x_max = 10;
const int y_max = 8;
const int x_min = 4;
const int y_min = 4;

// This Function assign region code for given point(x, y)
int assignRegionCode(double x, double y)
{
	int code = INSIDE;
	
	if (x < x_min) // to the left of rectangle
		code |= LEFT;
	else if (x > x_max) // to the right of rectangle
		code |= RIGHT;
	if (y < y_min) // below the rectangle
		code |= BOTTOM;
	else if (y > y_max) // above the rectangle
		code |= TOP;
	return code;
}

// Cohen Sutherland Line Clipping Algorithm
void cohenSutherlandAlgorithm(double x1, double y1, double x2, double y2)
{
	// Assigning region to endpoints of line
	int code1 = assignRegionCode(x1, y1);
	int code2 = assignRegionCode(x2, y2);
	bool accept = false;

// Repeat the process till line is completely outside or inside
	while (true) {
	    // Perform OR on endpoints
		if ((code1 | code2 ) ==0) {
			// If result is 0 then both endpoints lie within rectangle
			accept = true;
			break;
		}
		// Perform And on endpoints
		else if (code1 & code2) {
			// If result is not zero this means both endpoints are outside rectangle
			break;
		}
		else {
			// Line clipping required
			int code_out;
			double x, y;
           
           // The endpoint which does-not have region code 0000 is outside the view port
			if (code1 != 0)
				code_out = code1;
			else
				code_out = code2;

			// Find intersection point;
			// using formulas y = y1 + slope * (x - x1),
			// x = x1 + (1 / slope) * (y - y1)
			// Figure out region where endpoint lies
			if (code_out & TOP) {
				// point is above the clip rectangle
				x = x1 + (x2 - x1) * (y_max - y1) / (y2 - y1);
				y = y_max;
			}
			else if (code_out & BOTTOM) {
				// point is below the rectangle
				x = x1 + (x2 - x1) * (y_min - y1) / (y2 - y1);
				y = y_min;
			}
			else if (code_out & RIGHT) {
				// point is to the right of rectangle
				y = y1 + (y2 - y1) * (x_max - x1) / (x2 - x1);
				x = x_max;
			}
			else if (code_out & LEFT) {
				// point is to the left of rectangle
				y = y1 + (y2 - y1) * (x_min - x1) / (x2 - x1);
				x = x_min;
			}
			// Replace point outside rectangle by intersection point
			if (code_out == code1) {
				x1 = x;
				y1 = y;
				code1 = assignRegionCode(x1, y1);
			}
			else {
				x2 = x;
				y2 = y;
				code2 = assignRegionCode(x2, y2);
			}
		}
	}
	if (accept) {
		cout << "Line accepted from " << x1 << ", "
			<< y1 << " to " << x2 << ", " << y2 << endl;
		// Here the user can add code to display the rectangle
		// along with the accepted (portion of) lines
	}
	else
		cout << "Line rejected" << endl;
}

int main()
{
      // Line Clipping using Cohen Sutherland Line Clipping Algorithm
	cohenSutherlandAlgorithm(5, 5, 7, 7);
	cohenSutherlandAlgorithm(7, 9, 11, 4);
	cohenSutherlandAlgorithm(1, 5, 4, 1);

	return 0;
}

Complexity

The time and space complexity of Cohen Sutherland Line Clipping Algorithm are:

• Time complexity: O(n)
• Space complexity: O(1)

Conclusion

In this article we discussed Cohen Sutherland Line Clipping Algorithm and its implementation. We also discussed its c++ code implementation and its space and time complexities

Got a question or just want to chat? Comment below or drop by our forums, where a bunch of the friendliest people you’ll ever run into will be happy to help you out!