Table of Contents
ToggleIntroduction
Searching algorithms are essential in computer science for finding data in collections efficiently. Two fundamental search methods are linear search and binary search. While both algorithms have the same goal of locating an item in a collection, they go about it in very different ways. Understanding the key differences between these search techniques provides crucial insight into why some algorithms are more efficient than others.
This article will provide a difference between linear search and binary search and highlight their computational complexities. It will explain why binary search is a more efficient option for sorted data sets. We will discuss the advantages and limitations of each algorithm to demonstrate when one method should be favoured over the other.
Difference Between Linear Search And Binary Search
Linear and binary search are two fundamental search algorithms that take very different approaches to find target values in data sets. This article provides a comparative analysis between these two methods to highlight their key differences, advantages, and use cases.
| Metric | Linear Search | Binary Search |
|---|---|---|
| Order of Data | Works on both sorted and unsorted data | Requires sorted data |
| Time Complexity | O(n) worst case | O(log n) |
| Implementation | Simple | Complex |
| Speed | Slow on large data sets | Much faster than linear search |
| Use Cases | Small data sets, simplicity needed | Large sorted data sets, speed critical |
Efficiency and Speed: A Comparative Study
The most significant difference between linear and binary search is speed and complexity.
Linear search has a worst case time complexity of O(n) as it may need to scan all n elements in the worst case. The complexity remains O(n) even if the data is sorted.
Binary search has a much faster time complexity of O(log n) due to its divide-and-conquer approach. This provides exceptional speedups for large inputs.
For example, to search a sorted array of 1 million elements:
- Linear search would require 1 million comparisons (O(n))
- Binary search would only need around 20 comparisons (O(log n))
As data sets grow larger, binary search outperforms linear search by orders of magnitude in terms of speed.
Data Structure Suitability: When to Use Linear Search and When to Opt for Binary Search
Linear search is well-suited for smaller data sets where simplicity and flexibility outweighs search speed. Its simplicity also makes it the natural choice for searching unsorted data.
Binary search excels at searching large sorted data sets extremely quickly. It powers fast searches for databases, search engines, trees and more. The need for pre-sorted data is well worth the substantial speedup.
Complexity Matters: Understanding Time Complexity
The complexity classes O(n) vs O(log n) clearly demonstrate why binary search is vastly superior for large inputs. The log n growth of binary search makes it scale extremely well compared to the linear time complexity of sequential search.
Complexity analysis provides the foundation for choosing suitable algorithms and data structures that leverage efficient search methods like binary search. Understanding these core algorithmic differences is key to designing systems that can search data both quickly and efficiently.
Understanding the Basics
Let’s understand some basics of searching in data structures
Searching in Data Structures
Searching is one of the most fundamental operations in computer science and a key requirement for working with data structures and algorithms. Searching refers to the process of finding a particular item or data element within a larger collection or database. Efficient searching capabilities allow software systems and applications to quickly look up and retrieve information from large data sets.
Some common examples of search operations include:
- Finding a customer’s record in a database based on their ID number or name.
- Looking up a product by name or ID in an online store’s catalog.
- Locating a word in a dictionary to retrieve its definition.
- Searching a social network for other users that match specified criteria.
- Identifying records in a database that contain a particular keyword or value.
The ability to rapidly search collections and access desired elements is critical for building usable systems and software. Search operations form the foundation of many other key functions like sorting, filtering, and data analysis.
The Need for Different Search Methods
- Naively, one could search a collection by sequentially checking every single item until the target is found. This linear search approach works for small data sets but quickly becomes impractical as the number of elements increases.
- To enable efficient searching on large collections, computer scientists have developed a variety of algorithms with different trade-offs and complexities. The choice of search method depends heavily on the structure and organization of the data set.
Linear Search: A Deep Dive
Definition and Working Principle
Linear search is a sequential searching algorithm where we traverse a given data set element-by-element to find the target value. It starts by comparing the first item in the collection to the search key. If a match is found, the index/location of that item is returned. If not, the search continues onto the next element. This linear traversal of items continues until either the target is found or the end of the data set is reached.


For example, given the array [5, 2, 9, 1, 7], if we wanted to search for the value 1, the linear search would check each item beginning from index 0:
5 != 1
2 != 1
9 != 1
1 == 1 (Target found at index 3)
The linear search returns the location 3 once it finds the matching value.
Properties of Linear Search
Some key properties of linear search:
- Works on both sorted and unsorted data sets
- Worst case complexity is O(n) as it may require searching all n elements
- Best case complexity is O(1) if target is the first element
Code Implementation
Here is a Python implementation of linear search on a list:
def linear_search(arr, target):
for i in range(len(arr)):
if arr[i] == target:
return i
return -1Real-world Applications of Linear Search
Despite its simplicity, linear search is widely used in the real world due to its versatility and ease of implementation:
- Finding a contact in a phonebook or database by name
- Looking up dictionary words manually
- Searching keywords in a document or on a web page
- Checking if a number is present in a small array or list
Linear search shines for small data sets where simplicity and flexibility outweigh performance. It forms the basis of many everyday searching tasks.
Advantages and Limitations Of Linear Search
Key advantages of linear search:
- Simple implementation with minimal code
- Works on unsorted data
- Useful for small data sets
Major limitations:
- Performance degrades significantly for large inputs
- O(n) time complexity scales poorly as data size increases
- Does not utilize any existing structure in data
While simple and flexible, linear search can become extremely inefficient for searching large data sets compared to more advanced algorithms like binary search.
Binary Search: An In-depth Analysis
Definition and the Divide-and-Conquer Approach
Binary search is an efficient searching algorithm that leverages the property of a sorted data set to exponentially reduce the search space at each step.
It works by using the divide-and-conquer approach:
Begin by comparing the target value to the middle element of the sorted array.
If the target is equal to the middle element, return its index.
If not, determine which half of the array contains the target based on comparisons.
Repeat the process on the selected half until the target is found.
For example, given the sorted array [1, 5, 7, 9, 13, 19, 21], to search for 13:
9!= 13 —> eliminate low half
19!= 13 —> eliminate upper half
13 == 13 (Found at index 4)
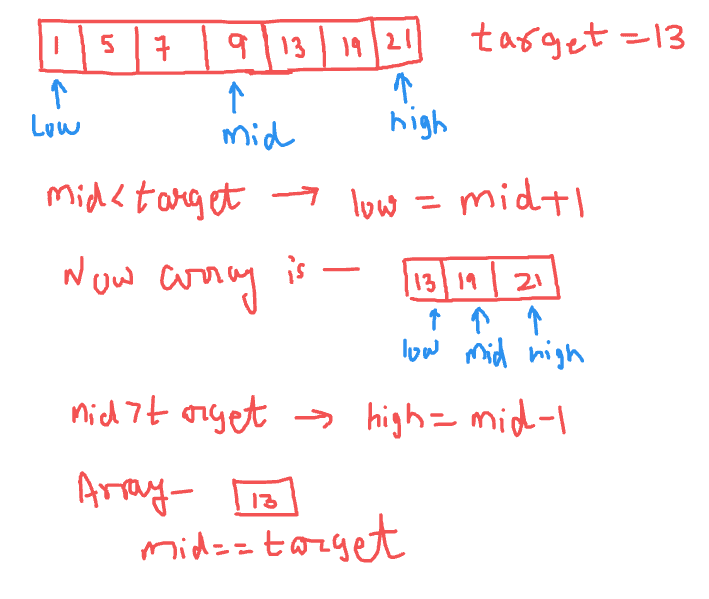
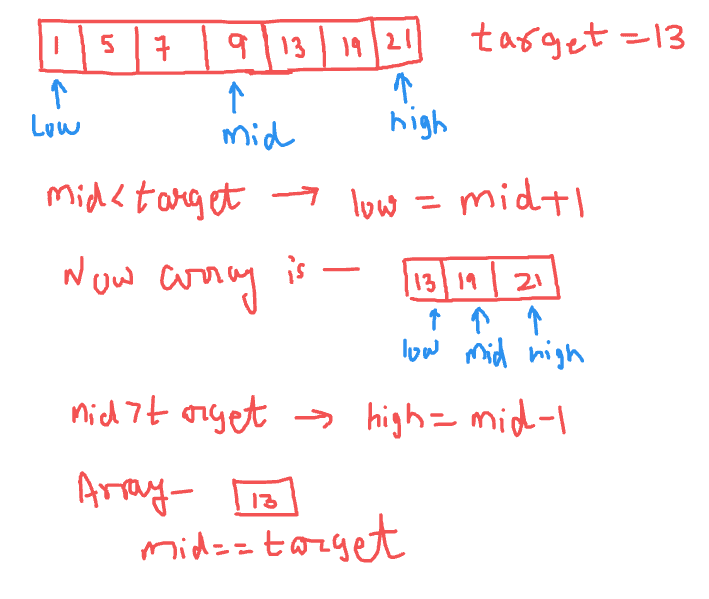
Instead of checking every element like linear search, the search space is cut in half at each step resulting in much faster search!
Properties Of Binary Search
The key aspects of binary search are:
- Applies to sorted data sets
- Runtime complexity of O(log n) for array of size n
- Utilizes divide-and-conquer approach to achieve speedup
Code Implementation
Here is an implementation in Python:
// Python Code for Binary Search
def binary_search(arr, target):
low = 0
high = len(arr) - 1
while low <= high:
mid = (low + high) // 2
if arr[mid] == target:
return mid
elif arr[mid] < target:
low = mid + 1
else:
high = mid - 1
return -1
Importance of Sorted Data Sets In Binary Search
A fundamental requirement for enabling binary search is that the data must be sorted. This allows reliably eliminating half of the search space at each step by comparing to the middle pivot element.
The trade-off is that real-world data is often unsorted and the cost of sorting must be accounted for. However, for data that is static or sorted once but searched many times, binary search provides substantial speedup.
Advantages and Limitations Of Binary Search
Key advantages of binary search:
- Much faster than linear search for large data sets
- O(log n) time complexity results in swift lookup
- Utilizes sorting structure of data for efficiency
Limitations:
- Requires sorted input data set
- Extra pre-processing step if data is unsorted
- Implementation is more complex than linear search
Overall, binary search provides exceptional search performance on sorted data. It powers fast lookups for databases, search engines and many optimized data structures.
Conclusion
Here is a conclusion summarizing the key takeaways on Difference Between Linear Search And Binary Search:
In summary, linear search and binary search represent two fundamental approaches to searching in computer science. While both algorithms aim to locate an item in a collection, they go about it in very different ways.
The key takeaways are:
- Linear search checks items sequentially, while binary search utilizes divide-and-conquer to eliminate subsets of data.
- Linear search works on unsorted data but has slow O(n) time complexity. Binary search is faster at O(log n) but requires sorted data.
- Linear search is better for small inputs where simplicity is preferred. Binary search wins for large data sets where speed is critical.
- Binary search provides immense speedups due to its logarithmic time complexity compared to the linear complexity of sequential search.
- Understanding the core distinctions between these basic algorithms lays the groundwork for making optimal choices around efficiency, data structures, and system design.
Try out our free resume checker service where our Industry Experts will help you by providing resume score based on the key criteria that recruiters and hiring managers are looking for.
Frequently Asked Questions (FAQs)
When should I use linear search vs binary search?
Use linear search when simplicity and flexibility is preferred over speed, such as for small data sets or unsorted data. Use binary search for large sorted datasets when faster search performance is critical.
Can binary search work on unsorted data?
No, binary search specifically requires the data to be sorted in order to work correctly. It relies on the ordering to quickly narrow down the search space each iteration.
Is binary search always faster than linear search?
Binary search is asymptotically faster with a complexity of O(log n) compared to O(n) for linear search. However, for very small data sets, the overhead of binary search may make linear search faster in practice.
What is the worst case complexity of linear search?
The worst case time complexity of linear search is O(n). This occurs when the item being searched for is not present in the data set or is the last element.
What are some real-world uses of linear search?
Everyday examples include searching contacts in a phonebook, keywords in a document, or looking up dictionary words manually. It’s a simple and flexible approach.
What data structures use binary search?
Binary search trees, sorted arrays, and balanced search trees rely on binary search for efficient lookup and retrieval operations. Database indexes also leverage binary search.
How is binary search implemented?
Binary search requires comparing the target to the middle pivot, eliminating one half based on comparison, and repeating on the remaining half until found.
What is the time complexity of binary search?
Binary search has a time complexity of O(log n). The search space is reduced by approximately 50% each iteration, resulting in very fast search times.


