How To Find Transpose Of A Matrix In C

Transpose of a matrix In C means converting its rows to columns and columns to rows. It is an important operation in linear algebra with applications in computing inverse matrices, solving systems of equations, and more. In this article, we will learn about matrices, see how to transpose a matrix In C, and implement matrix transposition algorithm in C.

What is a Matrix In C?

A matrix is a rectangular array of numbers arranged in rows and columns. For example:

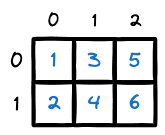
This is a 2 x 3 matrix with 2 rows and 3 columns. It has 6 elements in total.

Matrices are represented mathematically using the notation A(m x n) where m is the number of rows and n is the number of columns. The above matrix has dimensions 2 x 3 and can be denoted as:

A(2 x 3) = [1 3 5
            2 4 6]

Some key terms related to matrices:

• Order – Total number of rows x columns (2 x 3 = 6 for above matrix)
• Dimension – Number of rows x number of columns
• Diagonal – Top left to bottom right elements (1 and 6 here)

What Is Transpose Of A Matrix In C?

Transposing a matrix involves converting rows to columns and columns to rows. If A is the original matrix, then the transpose matrix is denoted as A^T.

For example, transposing the 2 x 3 matrix above results in a 3 x 2 matrix:

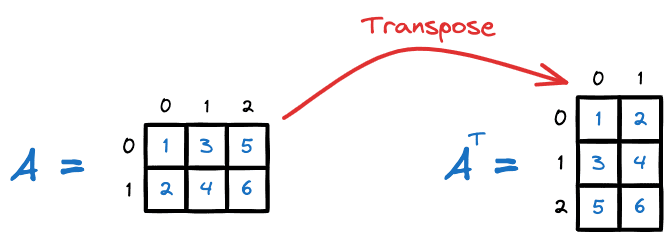
As we can see, the 1st row [1 3 5] became the 1st column and so on. The columns swapped with the rows.Transposing is useful for computing the inverse of a matrix, solving matrix equations, and more.

C Program To Find Transpose Of A Matrix

To Find the transpose of a Matrix In C:

Algorithm

• Initialise two loop variables, ‘i’ and ‘j’, to iterate through rows and columns.
• Use a nested loop structure with ‘i’ ranging from 0 to ‘m-1’ (number of rows) and ‘j’ ranging from 0 to ‘n-1’ (number of columns).
• Inside the nested loops:
  • The original matrix is traversed column wise and all the elements in a column are assigned to corresponding row of transpose matrix. Therefore, element at matrix[j][i] goes to transpose[i][j] cell.
  • Therefore, Assign the value of ‘matrix[j][i]’ (element at row ‘j’ and column ‘i’ of the original matrix) to ‘transpose[i][j]’ (element at row ‘i’ and column ‘j’ of the transposed matrix).
• Repeat this process for all elements of the matrix, effectively swapping the rows and columns to obtain the transposed matrix.

Code Implementation

// C Program To Find Transpose Of A Matrix

#include <stdio.h>

int main() {
    int m, n, i, j;

    // Input the number of rows (m) and columns (n) from the user
    printf("Enter the number of rows: ");
    scanf("%d", &m);
    printf("Enter the number of columns: ");
    scanf("%d", &n);

    int matrix[m][n];
    int transpose[n][m]; // Transposed matrix

    // Input the matrix elements
    printf("Enter the matrix elements:\n");
    for (i = 0; i < m; i++) {
        for (j = 0; j < n; j++) {
            scanf("%d", &matrix[i][j]);
        }
    }

    // Print the original matrix
    printf("Original Matrix:\n");
    for (i = 0; i < m; i++) {
        for (j = 0; j < n; j++) {
            printf("%d ", matrix[i][j]);
        }
        printf("\n");
    }

    // Calculate the transpose of the matrix
    for (i = 0; i < n; i++) {
        for (j = 0; j < m; j++) {
            transpose[i][j] = matrix[j][i];
        }
    }

    // Print the transposed matrix
    printf("Transpose Matrix:\n");
    for (i = 0; i < n; i++) {
        for (j = 0; j < m; j++) {
            printf("%d ", transpose[i][j]);
        }
        printf("\n");
    }

    return 0;
}

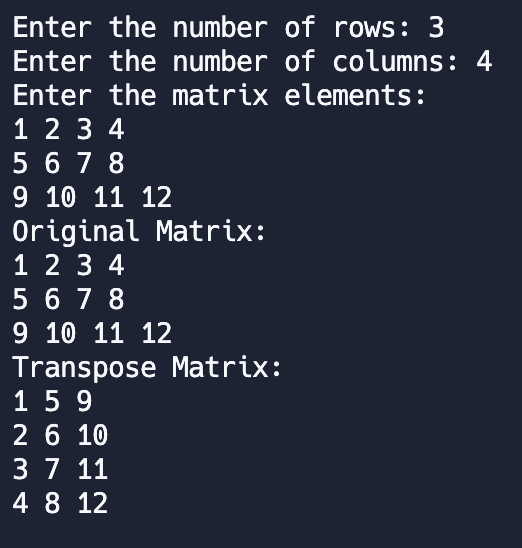
Output

Complexity Analysis

Time Complexity:

• Inputting the matrix elements takes O(m * n) time, where ‘m’ is the number of rows and ‘n’ is the number of columns.
• Calculating the transpose also takes O(m * n) time because each element of the original matrix is visited once.
• Printing the original and transposed matrices takes O(m * n) time.

The overall time complexity of the program is O(m * n).

Space Complexity:

• The space complexity is O(m * n) because two matrices, matrix and transpose, of size m x n are used to store the original and transposed matrices, respectively.

Key TakeAways

• Transpose of a matrix In C involves swapping its rows and columns.
• It can be done in-place by swapping diagonal elements directly.
• Transposing has applications in computing inverses, solving equations etc.

Checkout more C Tutorials here.

I hope You liked the post ?. For more such posts, ? subscribe to our newsletter. Try out our free resume checker service where our Industry Experts will help you by providing resume score based on the key criteria that recruiters and hiring managers are looking for.

FAQ