Table of Contents
ToggleIntroduction
Different types of sorting techniques are fundamental concepts in computer science that arrange data into a particular order, such as numerical order or lexicographic order. Efficient sorting is critical for optimising data retrieval, reducing search times, and streamlining many computational processes. This article provides a comprehensive overview of common types of sorting algorithms, their runtime complexity, advantages, use cases, and applications.
Fundamental Concepts
Sorting refers to algorithms that rearrange elements of a dataset into a specified order, such as ascending or descending. Sorting enables efficient searching, ordering, and selection operations to be performed on data.
The importance of efficient sorting cannot be understated. It enables databases to quickly order and retrieve records, search engines to return relevant results faster, and analytics applications to process data effectively.


Comparison Vs Non Comparison Based Types Of Sorting Algorithms
Types of Sorting algorithms are generally classified into comparison and non-comparison based algorithms. Comparison sorts evaluate the relative order of elements by directly comparing them. Non-comparison sorts use techniques like bucketing, counting Occurrences, or extracting digits to indirectly determine sort order.
| Parameter | Comparison Based Sorting | Non-Comparison Based Sorting |
|---|---|---|
| Basis of Sorting | Compares elements directly to determine order | Uses keys like digits, frequency etc. to determine order |
| Time Complexity | O(n2) for basic sorts, O(nlogn) for efficient sorts | O(n+k) for linear sorts, O(nk) for radix sort |
| Space Complexity | In-place possible e.g. quicksort | Use additional memory e.g. counting sort |
| Stability | Can be stable or unstable | Often stable |
| Data Types | General data types like integers, floats, strings etc. | Integers and distinct data types for counting, radix sorts |
| Examples | Insertion sort, merge sort, heapsort | Counting sort, radix sort, bucket sort |
| Comparisons | Direct comparison of elements | Sort based on keys like digit frequency |
| Implementation | Compare elements using comparisons operators | Count occurrences, extract digits, use buckets |
| Efficiency | Quadratic basic sorts, nlogn efficient sorts | Linear time possible for counting, bucket sorts |
| Extra Space | In-place sorting possible | Use additional arrays, buckets |
| Stability | Unstable possible e.g. quicksort | Often stable e.g. counting sort |
| Adaptability | Adaptive sorting possible e.g. timsort | Not adaptive, fixed algorithms |
| Parallelization | Challenging to parallelize | Better opportunities for parallelism |
Types of Sorting Algorithms
Elementary Sorting Algorithms
Elementary sorting algorithms conceptually demonstrate sorting, but have quadratic time complexity which limits efficiency.
Here are detailed explanations of bubble sort, selection sort, and insertion sort algorithms along with example working code implementations in Java, C, C++, and Python:
Bubble Sort
Bubble sort works by comparing adjacent elements in a list and swapping them if they are not in the intended order. This process is repeated until no more swaps are required, indicating the list is sorted.
Algorithm
Start with first element
Compare with next element, swap if not in order
Advance to next pair, repeat comparisons and swaps
Repeat process until no more swaps needed
Pseudocode
// PseudoCode For Bubble Sort
bubbleSort(arr[]):
n = length(arr)
for i = 0 to n-1 do:
for j = 0 to n-i-1 do:
if arr[j] > arr[j+1]
swap(arr[j], arr[j+1])Walkthrough
Consider the array [5, 1, 4, 2, 8]
- First pass:
- (5, 1) → swap since 5 > 1 → [1, 5, 4, 2, 8]
- (5, 4) → swap since 5 > 4 → [1, 4, 5, 2, 8]
- (5, 2) → swap since 5 > 2 → [1, 4, 2, 5, 8]
- (5, 8) → No swap
- Second pass:
- (4, 2) → swap since 4 > 2 → [1, 2, 4, 5, 8]
- (4, 5) → No swap
- (4, 8) → No swap
- Third pass:
- (2, 4) → swap since 2 < 4 → [1, 2, 4, 5, 8]
- No more swaps required, sorted.
After n-1 passes, array is sorted.
Properties
- Time Complexity: O(n2) worst and average case.
- Space Complexity: O(1), in-place sorting.
- Stable sorting algorithm.
- Simple implementation but highly inefficient for large data sets.
Code Examples
Java
// Types of Sorting algorithms : Bubble Sort Code in Java
void bubbleSort(int arr[]) {
int n = arr.length;
for(int i=0; i<n-1; i++) {
for(int j=0; j<n-i-1; j++) {
if(arr[j] > arr[j+1]) {
// swap elements
int temp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = temp;
}
}
}
}C
// Types of Sorting algorithms : Bubble Sort Code in C
void bubbleSort(int arr[], int n){
for(int i=0; i<n-1; i++){
for(int j=0; j<n-i-1; j++){
if(arr[j] > arr[j+1]){
// swap elements
int temp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = temp;
}
}
}
}C++
// Types of Sorting algorithms : Bubble Sort Code in C++
void bubbleSort(int arr[], int n){
for(int i=0; i<n-1; i++){
for(int j=0; j<n-i-1; j++){
if(arr[j] > arr[j+1]){
// swap elements
int temp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = temp;
}
}
}
}Python
# Types of Sorting algorithms : Bubble Sort Code in Python
def bubbleSort(arr):
n = len(arr)
for i in range(n-1):
for j in range(n-i-1):
if arr[j] > arr[j+1]:
# swap elements
arr[j], arr[j+1] = arr[j+1], arr[j]Selection Sort
Selection sort selects the minimum element from the unsorted portion in each pass and places it at the end of the sorted portion.
Algorithm
Set first element as minimum
Compare minimum to next element, change if smaller
After traversing array, swap minimum with first element
Repeat process reducing unsorted portion
Pseudocode
//PseudoCode for Selection Sort
selectionSort(arr[]):
n = length(arr)
for i = 0 to n-1 do:
minIndex = i
for j = i+1 to n do:
if arr[j] < arr[minIndex]
minIndex = j
swap(arr[i], arr[minIndex]) Walkthrough
Consider the array [5, 3, 1, 2, 4]
- First pass:
- Current min is index 0 (value 5)
- Iterate rest of array, update min to index 2 (value 1)
- After pass, swap 5 and 1 → [1, 3, 5, 2, 4]
- Second pass:
- Current min is index 1 (value 3)
- Iterate rest of array, no change in min
- After pass, no swap required → [1, 3, 5, 2, 4]
- Third pass:
- Current min is index 2 (value 5)
- Iterate rest of array, update min to index 3 (value 2)
- After pass, swap 5 and 2 → [1, 2, 5, 3, 4]
Repeat process, incrementing starting point each pass.
After n-1 passes, array is sorted.
Properties
- Time Complexity: O(n2) worst and average case.
- Space Complexity: O(1), in-place sorting.
- Unstable sorting algorithm.
- Simple implementation but inefficient for large data sets.
Code Examples
Java
// Types of Sorting algorithms: Selection Sort Code In Java
void selectionSort(int arr[]) {
int n = arr.length;
for(int i=0; i<n-1; i++) {
int min = i;
for(int j=i+1; j<n; j++){
if(arr[j] < arr[min]) {
min = j;
}
}
// Swap min element with first element
int temp = arr[min];
arr[min] = arr[i];
arr[i] = temp;
}
}C
// Types of Sorting algorithms: Selection Sort Code In C
void selectionSort(int arr[], int n) {
int i, j, min;
for(i=0; i<n-1; i++) {
min = i;
for(j=i+1; j<n; j++){
if(arr[j] < arr[min]) {
min = j;
}
}
// Swap min element with first element
int temp = arr[min];
arr[min] = arr[i];
arr[i] = temp;
}
}C++
// Types of Sorting algorithms: Selection Sort Code In C++
void selectionSort(int arr[], int n){
for(int i=0; i<n-1; i++){
int min = i;
for(int j=i+1; j<n; j++){
if(arr[j] < arr[min]){
min = j;
}
}
// Swap min element with first element
int temp = arr[min];
arr[min] = arr[i];
arr[i] = temp;
}
}Python
# Types of Sorting algorithms: Selection Sort Code In Python
def selectionSort(arr):
for i in range(len(arr)-1):
min = i
for j in range(i+1, len(arr)):
if arr[j] < arr[min]:
min = j
# Swap minimum with first element
arr[i], arr[min] = arr[min], arr[i]Insertion Sort
Insertion sort is a simple sorting algorithm that works by inserting each element into its correct position in the sorted portion of an array.
Algorithm
The array is virtually split into a sorted and unsorted portion. Initially, the sorted portion contains just the first element.
A current element is selected from the unsorted portion. This is compared to the elements in the sorted portion from right to left.
If the current element is greater than the element in the sorted portion, it is moved to the right. This process is repeated until an element smaller than the current is found.
Once the correct position for the current is found, it is inserted into the sorted portion.
Steps 2-4 are repeated for the remaining elements until the whole array is sorted.
Pseudocode
// Types of Sorting techniques: Psuedocode for Insertion Sort
For i = 1 to n-1
key = arr[i]
j = i-1
While j >= 0 and arr[j] > key
arr[j+1] = arr[j]
j = j-1
arr[j+1] = keyWalkthrough
Consider the array [5, 2, 4, 6, 1, 3]
- Start by assuming first element 5 is sorted. Unsorted portion is [2, 4, 6, 1, 3]
- Take 2 as current element. Compare with 5. 2 < 5, so move 5 to right. Insert 2 before 5. Sorted portion is [2, 5].
- Take 4 as current element. Compare with 5 and 2. Stop at 2 which is smaller. Insert 4 after 2. Sorted portion is [2, 4, 5].
- Take 6 as current element. Compare with 5. 6 > 5, so insert after 5. Sorted portion is [2, 4, 5, 6].
- Take 1 as current element. Compare with 6, 5, 4, 2. Insert before 2. Sorted portion is [1, 2, 4, 5, 6].
- Take 3 as current element. Insert after 2. Sorted portion is [1, 2, 3, 4, 5, 6].
Properties
- Space complexity: O(1), in-place sorting
- Stable sorting algorithm
- Adaptive algorithm – efficient for partially sorted data
- Best Case: O(n) – Array is already sorted
- Average Case: O(n^2)
- Worst Case: O(n^2)
Insertion sort is simple to implement but inefficient for large data sets. It is more efficient than bubble sort and selection sort. The algorithm is stable and adaptive, making it useful in practice, especially when data is mostly sorted.
Code Example
Java
// Types of Sorting techniques: Insertion Sort Code in Java
void insertionSort(int arr[]) {
for(int i=1;i<arr.length;i++){
int temp = arr[i];
int j = i-1;
while(j>=0 && arr[j]>temp){
arr[j+1] = arr[j];
j--;
}
arr[j+1] = temp;
}
}C
// Types of Sorting techniques: Insertion Sort Code in C
void insertionSort(int arr[], int n){
for(int i=1; i<n; i++){
int temp = arr[i];
int j = i-1;
while(j>=0 && arr[j]>temp){
arr[j+1] = arr[j];
j--;
}
arr[j+1] = temp;
}
}C++
// Types of Sorting techniques: Insertion Sort Code in C++
void insertionSort(int arr[], int n){
for(int i=1; i<n; i++){
int temp = arr[i];
int j = i-1;
while(j>=0 && arr[j]>temp){
arr[j+1] = arr[j];
j--;
}
arr[j+1] = temp;
}
}Python
# Types of Sorting techniques: Insertion Sort Code in Python
def insertionSort(arr):
for i in range(1, len(arr)):
temp = arr[i]
j = i-1
while j>=0 and arr[j]>temp:
arr[j+1] = arr[j]
j -= 1
arr[j+1] = tempEfficient Sorting Algorithms
Efficient algorithms use techniques like divide-and-conquer to achieve improved time complexities compared to elementary algorithms.
Merge Sort
Merge sort works by recursively splitting the array into halves, sorting each half, and merging them back together in sorted order.
Algorithm
If the array has 0 or 1 element, it is already sorted. Otherwise, split the array in half.
Recursively sort each half by repeating the splitting process until arrays of 0 or 1 element are reached.
Merge the sorted subarrays together to produce the final sorted array.
Merge Process:
- Create pointers for first elements of each array. Compare elements, add smaller one to output.
- Advance pointer of array whose element was added. When a pointer reaches end of an array, add remaining elements of other array.
PseudoCode
// Types of Sorting techniques: PseudoCode for Merge Sort
mergeSort(arr[], left, right):
if right > left:
mid = (left + right)/2
mergeSort(arr, left, mid)
mergeSort(arr, mid+1, right)
merge(arr, left, mid, right)
merge(arr[], left, mid, right):
create temp arrays L[] and R[]
copy arr elements to L[] and R[]
i = j = k = 0
while i < n1 and j < n2:
if L[i] <= R[j]:
arr[k] = L[i]
i++
else:
arr[k] = R[j]
j++
k++
copy remaining elements of L[] and R[] to arr[] Walkthrough
Consider the array [38, 27, 43, 3, 9, 82, 10]
- Divide array into [38, 27, 43, 3] and [9, 82, 10]
- Divide first subarray into [38, 27] and [43, 3] and second subarray into [9] and [82, 10]
- Merge [38, 27] and [43, 3] into [3, 27, 38, 43]
- Merge [9] and [82, 10] into [9, 10, 82]
- Merge previous sorted arrays into [3, 9, 10, 27, 38, 43, 82]
Properties
- Space complexity: O(n) auxiliary
- Stable sorting algorithm
- In-place merging is complex
- Worst case performance: O(nlogn)
Overall, merge sort is an efficient, stable sorting algorithm optimal for larger datasets. Its divide and conquer strategy reduces time complexity.
Code Examples
Java
// Types of Sorting techniques: Merge Sort Code in Java
void mergeSort(int arr[], int l, int r) {
if (l < r) {
int m = l+(r-l)/2;
mergeSort(arr, l, m);
mergeSort(arr, m+1, r);
merge(arr, l, m, r);
}
}
void merge(int arr[], int l, int m, int r) {
// Merge code
}C
// Types of Sorting techniques: Merge Sort Code in C
void mergeSort(int arr[], int l, int r){
if(l < r){
int m = l+(r-l)/2;
mergeSort(arr, l, m);
mergeSort(arr, m+1, r);
merge(arr, l, m, r);
}
}
void merge(int arr[], int l, int m, int r){
// Merge code
}C++
// Types of Sorting techniques: Merge Sort Code in C++
void mergeSort(int arr[], int l, int r){
if(l < r){
int m = l+(r-l)/2;
mergeSort(arr, l, m);
mergeSort(arr, m+1, r);
merge(arr, l, m, r);
}
}
void merge(int arr[], int l, int m, int r){
// Merge code
}Python
# Types of Sorting techniques: Merge Sort Code in Python
def mergeSort(arr,l,r):
if l < r:
m = (l+(r-1))//2
mergeSort(arr, l, m)
mergeSort(arr, m+1, r)
merge(arr, l, m, r)
def merge(arr, l, m, r):
# Merge code Quicksort
Quicksort is an efficient divide and conquer sorting algorithm. It works by selecting a ‘pivot’ element and partitioning the array around it such that elements less than the pivot are to the left and greater elements are to the right.
Algorithm
Select the last element as pivot
Partition the array by placing elements less than pivot to the left and greater than pivot to the right of pivot.
Recursively apply the same process to left and right subarrays.
Partitioning:
- Initialize left pointer at first element and right pointer at last element.
- Increment left pointer until an element greater than pivot is found. Increment right pointer until an element less than pivot is found.
- Swap the elements and repeat process until pointers cross.
- Place pivot between the pointers.
Pivot Selection:
- First, middle or random element can be picked as pivot. Last element is commonly used.
- Median of medians method provides optimal pivot selection.
Pseudocode
// Types of Sorting techniques: Pseudocode for QuickSort
quickSort(arr[], low, high) {
if (low < high) {
pivotIndex = partition(arr, low, high)
quickSort(arr, low, pivotIndex)
quickSort(arr, pivotIndex + 1, high)
}
}
partition(arr[], low, high) {
// Partitioning logic
return pivotIndex;
}Walkthrough
Consider the array [9, 6, 5, 3, 1, 8, 7, 2, 4]
- Select last element 4 as pivot
- Initialization: Left pointer = 0, right pointer = 8
- Increment left pointer to 1, swap 9 and 6
- Array: [6, 9, 5, 3, 1, 8, 7, 2, 4]
- Increment right pointer to 7, swap 4 and 2
- Array: [6, 9, 5, 3, 1, 8, 2, 7, 4]
- Increment left pointer to 3, swap 5 and 3
- Array: [6, 9, 3, 5, 1, 8, 2, 7, 4]
- Pointers crossed. Pivot placed between them.
- Array: [3, 2, 1, 5, 6, 8, 9, 7, 4]
- Quicksort applied recursively on subarrays [3, 2, 1] and [5, 6, 8, 9, 7]
Properties
- Time Complexity:
- Best case: O(nlogn)
- Average case: O(nlogn)
- Worst case: O(n^2)
- Space Complexity: O(logn)
- In place sorting algorithm
- Unstable sorting algorithm
Quicksort is efficient in practice, provides good average case performance and extra space usage is only for recursive calls. However, worst case is quadratic making it unsuitable for certain scenarios.
Code Examples
Java
// Types of Sorting techniques: Quick Sort Java Program
void quickSort(int arr[], int low, int high) {
if (low < high) {
int pivot = partition(arr, low, high);
quickSort(arr, low, pivot-1);
quickSort(arr, pivot+1, high);
}
}
int partition(int arr[], int low, int high) {
int pivot = arr[high];
int i = (low-1);
for (int j=low; j<high; j++) {
if (arr[j] <= pivot) {
i++;
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
int temp = arr[i+1];
arr[i+1] = arr[high];
arr[high] = temp;
return i+1;
}C++
// Types of Sorting techniques: Quick Sort Java Program C++
void quickSort(int arr[], int low, int high) {
if (low < high) {
int pivot = partition(arr, low, high);
quickSort(arr, low, pivot-1);
quickSort(arr, pivot+1, high);
}
}
int partition (int arr[], int low, int high) {
int pivot = arr[high];
int i = (low - 1);
for (int j = low; j < high; j++) {
if (arr[j] <= pivot) {
i++;
swap(arr[i], arr[j]);
}
}
swap(arr[i+1], arr[high]);
return (i+1);
}C
// Types of Sorting techniques: Quick Sort Java Program C
void quickSort(int arr[], int low, int high){
if (low < high) {
int pivot = partition(arr, low, high);
quickSort(arr, low, pivot-1);
quickSort(arr, pivot+1, high);
}
}
int partition (int arr[], int low, int high) {
int pivot = arr[high];
int i = (low - 1);
for (int j = low; j < high; j++) {
if (arr[j] <= pivot) {
i++;
swap(&arr[i], &arr[j]);
}
}
swap(&arr[i+1], &arr[high]);
return (i+1);
}Python
// Types of Sorting techniques: Quick Sort Java Program Python
def quickSort(arr, low, high):
if low < high:
pivot = partition(arr, low, high)
quickSort(arr, low, pivot-1)
quickSort(arr, pivot+1, high)
def partition(arr, low, high):
pivot = arr[high]
i = low-1
for j in range(low, high):
if arr[j] <= pivot:
i += 1
arr[i], arr[j] = arr[j], arr[i]
arr[i+1], arr[high] = arr[high], arr[i+1]
return i+1Heapsort
Heapsort uses a binary heap data structure to efficiently sort an array. It converts the array into a max heap, repeatedly extracts the maximum element, and places it at the end of the array.
Algorithm Of Heap Sort
Convert the array into a max heap by heapifying it from the midpoint down to the first element.
Swap the root (maximum value) with the last element of the heap.
Discard the last element from the heap and readjust to maintain max heap property.
Repeat steps 2 and 3 reducing the heap size by 1 each time until only one element remains.
Heapify
The heapify procedure converts a subtree into a max heap by comparing nodes with children and swapping if necessary to maintain the heap order property.
Build Max Heap
Heapify is called on each subtree from midpoint to first element to convert the full array into a max heap.
Pseudocode
// Types of Sorting techniques : PseudoCode and algorithm of heap sort
heapSort(arr):
buildMaxHeap(arr)
for i = n to 1:
swap arr[1] and arr[i]
heapify(arr, 1, i-1)
buildMaxHeap(arr):
for i = n/2 to 1:
heapify(arr, i, n)
heapify(arr, i, n):
largest = i
l = 2*i, r = 2*i + 1
if l <= n and arr[l] > arr[largest]:
largest = l
if r <= n and arr[r] > arr[largest]:
largest = r
if largest != i:
swap arr[i] and arr[largest]
heapify(arr, largest, n)Walkthrough
Consider the array [6, 5, 3, 7, 2, 8, 4]
- Heapify subtree [5, 3]: Swap 5 and 3 since 3 is larger. Heap is [6, 3, 5, 7, 2, 8, 4]
- Heapify subtree [6, 3, 5]: No change needed.
- Heapify full array from midpoint: [8, 6, 7, 4, 2, 5, 3]
- Swap root 8 with last element 3: [3, 6, 7, 4, 2, 5, 8]
- Discard 8, heapify reduced heap: [5, 6, 7, 4, 2, 3]
- Swap root 5 with last element 2: [2, 6, 7, 4, 3, 5]
- Discard 5, heapify: [4, 6, 7, 2, 3]
- Continue process until 1 element left: [2, 3, 4, 5, 6, 7, 8]
The heapsort algorithm efficiently sorts the array in O(nlogn) time by exploiting the heap data structure.
Code Examples
Java
// Types of Sorting algorithms : Heap Sort
void heapSort(int[] arr, int n) {
// heapify
for (int i = n/2 - 1; i >= 0; i--)
heapify(arr, n, i);
// extract elements
for (int i=n-1; i>=0; i--) {
int temp = arr[0];
arr[0] = arr[i];
arr[i] = temp;
heapify(arr, i, 0);
}
}C++
// Heap Sort C++
void heapSort(int arr[], int n) {
// heapify
for (int i = n/2 - 1; i >= 0; i--)
heapify(arr, n, i);
// extract elements
for (int i=n-1; i>=0; i--) {
int temp = arr[0];
arr[0] = arr[i];
arr[i] = temp;
heapify(arr, i, 0);
}
}C
// Heap Sort in C
void heapSort(int arr[], int n) {
// heapify
for (int i = n/2 - 1; i >= 0; i--) {
heapify(arr, n, i);
}
// extract elements
for (int i=n-1; i>=0; i--) {
int temp = arr[0];
arr[0] = arr[i];
arr[i] = temp;
heapify(arr, i, 0);
}
}Python
# Heap Sort
def heapify(arr, n, i):
# heapify logic
def heapSort(arr):
n = len(arr)
# heapify
for i in range(n//2 - 1, -1, -1):
heapify(arr, n, i)
# extract elements
for i in range(n-1, 0, -1):
arr[i], arr[0] = arr[0], arr[i]
heapify(arr, i, 0)Non-Comparison Based Sorting
Non-comparison sorts use alternative techniques like counting, radixes, or bucketing. These allow improved efficiency for certain data types.
Here are detailed explanations of counting sort, bucket sort, radix sort, timsort and shellsort algorithms including the algorithm, walkthrough and properties:
Counting Sort
Counting sort is an efficient non-comparison sorting algorithm that sorts elements in linear time by determining the count of each unique element in the array.
Algorithm
Find the maximum and minimum values in the array to determine the range of elements.
Create a count array/list of size equal to the range, with all values initialized to 0.
Iterate through the input array and increment count[i] for each element with value i.
Modify count such that each index stores the cumulative sum of previous counts.
Output each element from input array by looking up its index/count in count array.
Pseudocode
// Types of Sorting algorithms: Pseudocode for counting sort
countSort(array):
max = find largest element in array
min = find smallest element in array
count = create array of size (max-min+1) with all 0s
for each element in array:
count[element]++
for i = 1 to max-min:
count[i] += count[i-1]
for i = n-1 to 0:
output[count[array[i]]-1] = array[i]
count[array[i]]--
return outputWalkthrough
Input array: [1, 4, 7, 3, 4, 6, 4]
- Find min and max values as 1 and 7
- Create count array of size 7: [0, 0, 0, 0, 0, 0, 0]
- Update count array based on input: [0, 2, 1, 1, 0, 1, 2]
- Cumulative counts: [0, 2, 3, 4, 4, 5, 7]
- Output array using count: [1, 3, 6, 4, 4, 4, 7]
Code Examples
Java
// Types of Sorting algorithms: Counting Sort In Java
void countingSort(int[] arr) {
int max = Arrays.stream(arr).max().getAsInt();
int min = Arrays.stream(arr).min().getAsInt();
int range = max - min + 1;
int count[] = new int[range];
int output[] = new int[arr.length];
// count occurrences
for (int i = 0; i < arr.length; i++) {
count[arr[i] - min]++;
}
// cumulative count
for (int i = 1; i < count.length; i++) {
count[i] += count[i - 1];
}
// fill output array
for (int i = arr.length - 1; i >= 0; i--) {
output[count[arr[i] - min] - 1] = arr[i];
count[arr[i] - min]--;
}
}C++
// Types of Sorting algorithms: Counting Sort In C++
void countingSort(int arr[], int n) {
int max = *max_element(arr, arr+n);
int min = *min_element(arr, arr+n);
int range = max - min + 1;
int count[range], output[n];
fill(count, count + range, 0);
// store counts
for (int i = 0; i < n; i++)
count[arr[i]-min]++;
// cumulative counts
for (int i = 1; i < range; i++)
count[i] += count[i-1];
// fill output array
for (int i = n-1; i >= 0; i--) {
output[count[arr[i]-min]-1] = arr[i];
count[arr[i]-min]--;
}
}C
// Types of Sorting algorithms: Counting Sort In C
void countingSort(int arr[], int n) {
int max = arr[0];
for (int i = 1; i < n; i++) {
if (arr[i] > max)
max = arr[i];
}
int min = arr[0];
for (int i = 1; i < n; i++) {
if (arr[i] < min)
min = arr[i];
}
int range = max - min + 1;
int count[range];
int output[n];
for (int i = 0; i < range; i++) {
count[i] = 0;
}
// store counts of each element
for (int i = 0; i < n; i++) {
count[arr[i] - min]++;
}
// cumulative counts
for (int i = 1; i < range; i++) {
count[i] += count[i - 1];
}
// fill output array
for (int i = 0; i < n; i++) {
output[count[arr[i] - min] - 1] = arr[i];
count[arr[i] - min]--;
}
}
Python
# Types of Sorting algorithms: Counting Sort In Python
def countingSort(arr):
max_val = max(arr)
min_val = min(arr)
range_val = max_val - min_val + 1
count = [0 for _ in range(range_val)]
output = [0 for _ in range(len(arr))]
# store count of each element
for i in arr:
count[i-min_val] += 1
# cumulative counts
for i in range(1, len(count)):
count[i] += count[i-1]
# fill output array
for i in range(len(arr)-1, -1, -1):
output[count[arr[i] - min_val] - 1] = arr[i]
count[arr[i] - min_val] -= 1
for i in range(len(arr)):
arr[i] = output[i]Properties:
- Time Complexity: O(n+k) where n is number of elements, k is range of input
- Space Complexity: O(n+k) for count array
- Stable sorting algorithm
- Efficient for small integer keys within a specific range
- Not in-place, requires extra memory
Counting sort works well for sorting small positive integers with a tight range by exploiting the frequency data of input elements.
Bucket Sort
Bucket sort partitions elements into buckets representing ranges, then sorts each bucket individually.
Algorithm
Initialize buckets covering value range
Distribute elements into buckets
Sort individual buckets using any sorting algorithm
Concatenate buckets in order
Pseudocode
// Types of Sorting algorithms: Pseudocode for bucketsort bucketSort(array, k): // k is the number of buckets initialize k empty buckets for each element in array: insert element into appropriate bucket for i = 1 to k: sort elements in bucket i using insertion sort concatenate sorted buckets return concatenated array
Walkthrough
Original array: [0.25, 0.5, 0.75, 0.1]
Bucket ranges: [0-0.25), [0.25-0.5), [0.5-0.75), [0.75-1]
Distribute into buckets:
B1: [0.1]
B2: [0.25]
B3: [0.5, 0.75]
Sort buckets:
B1: [0.1]
B2: [0.25]
B3: [0.5, 0.75]
Concatenate: [0.1, 0.25, 0.5, 0.75]
Properties
- Time Complexity: O(n+k)
- Space Complexity: O(n+k)
- Stable sort based on sub-sort
Bucket allows sorting of floats and non-uniform distributions efficiently.
Code Examples
Java
// Types of Sorting algorithms: Bucket Sort In Java
void bucketSort(float[] arr) {
int n = arr.length;
@SuppressWarnings("unchecked")
List<Float>[] buckets = new List[n];
// initialize buckets
for (int i = 0; i < n; i++) {
buckets[i] = new ArrayList<>();
}
// distribute elements into buckets
for (int i = 0; i < n; i++) {
int bucketIdx = (int)arr[i] * n;
buckets[bucketIdx].add(arr[i]);
}
// sort individual buckets
for (int i = 0; i < n; i++) {
Collections.sort(buckets[i]);
}
// concatenate buckets
int index = 0;
for (int i = 0; i < n; i++) {
for (int j = 0, size = buckets[i].size(); j < size; j++) {
arr[index++] = buckets[i].get(j);
}
}
}C
// Types of Sorting algorithms: Bucket Sort In C
void bucketSort(float arr[], int n) {
int i, j;
float buckets[n][n];
// put elements into buckets
for (i = 0; i < n; i++) {
int bucketIdx = n * arr[i];
buckets[bucketIdx][j++] = arr[i];
}
// sort individual buckets
for (i = 0; i < n; i++) {
qsort(buckets[i], j, sizeof(float), compare);
}
// concatenate buckets
j = 0;
for (i = 0; i < n; i++) {
int k;
for (k = 0; k < n; k++) {
arr[j++] = buckets[i][k];
}
}
}C++
// Types of Sorting algorithms: Bucket Sort In C++
void bucketSort(float arr[], int n) {
vector<float> buckets[n];
// put elements in buckets
for (int i=0; i<n; i++) {
int bucketIdx = arr[i] * n;
buckets[bucketIdx].push_back(arr[i]);
}
// sort individual buckets
for (int i = 0; i < n; i++)
sort(buckets[i].begin(), buckets[i].end());
// concatenate buckets
int index = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j < buckets[i].size(); j++) {
arr[index++] = buckets[i][j];
}
}
}
Python
# Types of Sorting algorithms: Bucket Sort In Python
def bucketSort(arr):
max_val = max(arr)
size = len(arr)
buckets_list = [[] for _ in range(size)]
# put elements in different buckets
for i in range(size):
j = int(size * arr[i])
if j != size:
buckets_list[j].append(arr[i])
else:
buckets_list[size - 1].append(arr[i])
# sort individual buckets
for i in range(size):
buckets_list[i] = sorted(buckets_list[i])
# concatenate buckets
k = 0
for i in range(size):
for j in range(len(buckets_list[i])):
arr[k] = buckets_list[i][j]
k += 1
return arrRadix Sort
Radix sort stably sorts array by digits at each position iteratively from least to most significant.
Algorithm
- Extract digits from same position using digit as key
- Sort array using digit key
- Repeat for next digit positions
Pseudocode
// Types of Sorting algorithms: Pseudocode For Radixsort radixSort(array, d): // d is number of digits in largest number for i = 1 to d: use counting sort on array by ith digit return array
Walkthrough
Array: 329, 457, 657, 839, 436, 720
Ones place: [9, 7, 7, 9, 6, 0] -> [720, 329, 436, 839, 457, 657]
Tens place: [329, 436, 457, 657, 720, 839]
Hundreds place: [329, 436, 457, 657, 720, 839]
Properties
- Time Complexity: O(nk)
- Space Complexity: O(n+k)
- Stable sort
Radix efficiently sorts integers stably in linear time.
Code Example
Java
// Types of Sorting algorithms: Radix Sort
void radixSort(int[] arr) {
int max = Arrays.stream(arr).max().getAsInt();
// sort by each digit
for (int exp = 1; max/exp > 0; exp *= 10) {
countSort(arr, exp);
}
}
void countSortForRadix(int[] arr, int exp) {
// count sort logic using digit at exp
}C
// Types of Sorting algorithms: Radix Sort
void radixSort(int arr[], int n) {
int m = getMax(arr, n);
// sort by each digit
for (int exp = 1; m/exp > 0; exp *= 10) {
countSort(arr, n, exp);
}
}
// count sort logic for radixC++
// Types of Sorting algorithms: Radix Sort
void radixSort(int arr[], int n) {
int max = *max_element(arr, arr+n);
// sort by each digit
for (int exp = 1; max/exp > 0; exp *= 10)
countSort(arr, n, exp);
}
void countSort(int arr[], int n, int exp) {
// count sort logic on digit at exp
}Python
# Types of Sorting algorithms: Radix Sort
def countingSortForRadix(exp, arr):
# count sort logic for radix
def radixSort(arr):
max_element = max(arr)
place = 1
while max_element // place > 0:
countingSortForRadix(place, arr)
place *= 10Shellsort
Shellsort sorts array by comparing elements separated by gaps that are reduced each iteration.
Algorithm
Initialize gap value
Sort array using insertion sort and gap
Reduce gap and repeat sorting
Pseudocode
// PseudoCode For Shell Sort shellSort(array, n): initialize gap = n/2 while gap > 0: for i = gap to n: insert array[i] among previous using insertion sort and gap reduce gap to gap/2 return array
Shell sort improves on insertion sort by comparing across gaps.
Properties
- Time Complexity: O(nlogn) down to O(n^1.25)
- Space Complexity: O(1)
- Unstable sort
Shell sort code
Timsort
Timsort combines insertion sort and mergesort. It sorts small chunks with insertion sort, then merges the chunks.
Algorithm
Divide array into sorted chunks with insertion sort
Merge chunks using mergesort when they reach threshold size
Properties
- Time Complexity: O(n log n)
- Space Complexity: O(n)
- Stable sort
- Adaptive optimization for real-world data
Timsort is optimized for performance on many real-world datasets.
Sorting in Programming Languages
Built-in sorting functions and libraries are optimized for convenience and efficiency.
Here are different ways of using different types of sorting in different programming languages:
Python
sorted()– Returns a sorted list from an iterablelist.sort()– Sorts a list in-place- Uses Timsort (hybrid of mergesort and insertion sort)
keyandreverseparams for custom sorting logic
Java
Arrays.sort()– Sorts primitive arraysCollections.sort()– Sorts object collections- Uses optimized quicksort and merge sort implementations
Comparatorinterfaces for custom sorting
C++
std::sort()– General purpose sort functionstd::stable_sort()– Stable sort function- Internally uses introsort – introspective sort
- Overload comparison operators or provide comparator function for custom sorts
Types of Sorting In C
qsort()– Implements quicksort algorithmcomparatorfunction required for custom sorting logic- Not a stable sort
- Pointer friendly for arrays
JavaScript
array.sort()– Sorts array in-placecompareFunctionoptional for custom sort order- Uses quicksort V8 engine optimization
- Works on any iterable objects
Go
sortpackage –Sort()andStable()functionssort.Interfaceinterface for custom sorts- Hybrid merge+insertion sort for efficiency
- Concurrency-safe versions available
Most languages provide built-in highly optimised sorting functions while allowing customisation like comparator functions.
Comparison of Different Types Of Sorting Techniques
Here is a comparison of different types of sorting techniques :
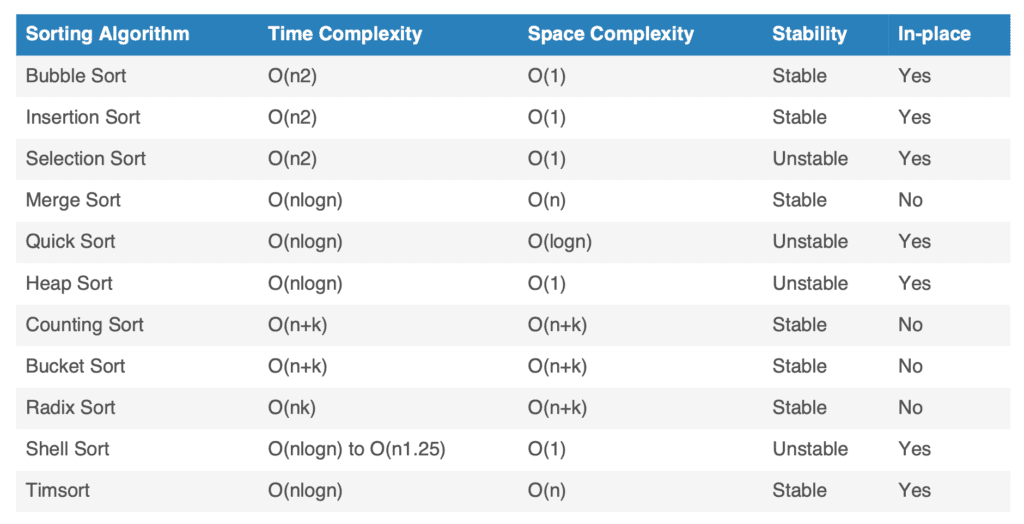

- Bubble, insertion and selection sorts are elementary sorts with quadratic time complexity.
- Merge, quick, heap are efficient general purpose sorts with O(nlogn) complexity.
- Counting, bucket and radix exploit properties of input for improved efficiency.
- Shell and timsort use hybrid approaches for real-world optimization.
- Stability, in-place requirements, input size etc. factor into choosing the best sort.
Applications of Sorting
- Databases rely on efficient sorting for quickly ordering and indexing records.
- Web search engines use sorting to return most relevant results first.
- Analytics tasks require sorting for summarization, pattern analysis, and data processing.
Conclusion
Sorting is an essential concept in computer science with widespread applications. Efficient sorting enables processing and retrieval of data in diverse computing areas. Further exploration of advanced sorting, implementations, and real-world use cases is encouraged.In this articile we covered types of sorting algorithms along with algorithms and code in various programming language.
Try out our free resume checker service where our Industry Experts will help you by providing resume score based on the key criteria that recruiters and hiring managers are looking for.
References
- Introduction to Algorithms by Thomas H. Cormen et al.
- Algorithms by Robert Sedgewick and Kevin Wayne
- The Art of Computer Programming by Donald Knuth
FAQ Regarding Types Of Sorting Techniques
When should I use a stable vs unstable sorting algorithm?
Stable algorithms maintain order of elements with equal keys. Use stable sort when relative order needs to be maintained, like sorting names by surname.
When would bucket sort be more efficient than quicksort?
Bucket sort works well when input is uniformly distributed. It can achieve linear time complexity compared to quicksort’s nlogn.
What are some examples of adaptive sorting algorithms?
Timsort and introsort are examples of adaptive sorts that can optimize based on partially sorted data.
How does radix sort achieve linear time complexity?
Radix sort exploits the integer digit structure by sorting on each position iteratively. This avoids comparisons between elements.
What is a hybrid sorting algorithm?
Hybrid algorithms combine approaches from multiple sorting techniques like timsort using insertion sort and merge sort.


