Table of Contents
ToggleThe process of cutting the part of line lying outside the view pane is called line clipping. The following algorithms are used for line clipping:
- Cohen Sutherland Line Clipping Algorithm
- Liang-Barsky Line Clipping Algorithm
- Midpoint Subdivision Line Clipping Algorithm
In this article we will focus on Cohen Sutherland Line Clipping Algorithm and its implementation
Viewport
The viewport is a region of the window in which graphics are displayed.
Problem Statement
Given a set of lines and a view pane, clip the lines that are outside the area of interest. If line is completely outside remove the line.
Input : View Pane coordinates
x_min = 4, y_min = 4, x_max = 10, y_max = 8
Set of line coordinates
line 1 : x1 = 5, y1 = 5, x2 = 7, y2 = 7
Line 2 : x1 = 7, y1 = 9, x2 = 11, y2 = 4
Line 3 : x1 = 1, y1 = 5, x2 = 4, y2 = 1
Output :
Line 1 : Accepted Line accepted from (5, 5) to (7, 7)
Line 2 : Accepted Line accepted from (7.8, 8) to (10, 5.25)
Line 3 : Rejected
Cohen Sutherland Line Clipping Algorithm
In Cohen Sutherland Line Clipping Algorithm the viewing space is divided into nine encoded regions. For each endpoint of a line segment, we assign a 4-bit code following the rules below
- bit 1 is 1 if x<Xmin
- bit 2 is 1 if x>Xmax
- bit 3 is 1 if y< Ymin
- bit4 is1 if y>Ymax
So, based on above rule the regions with code will look like below
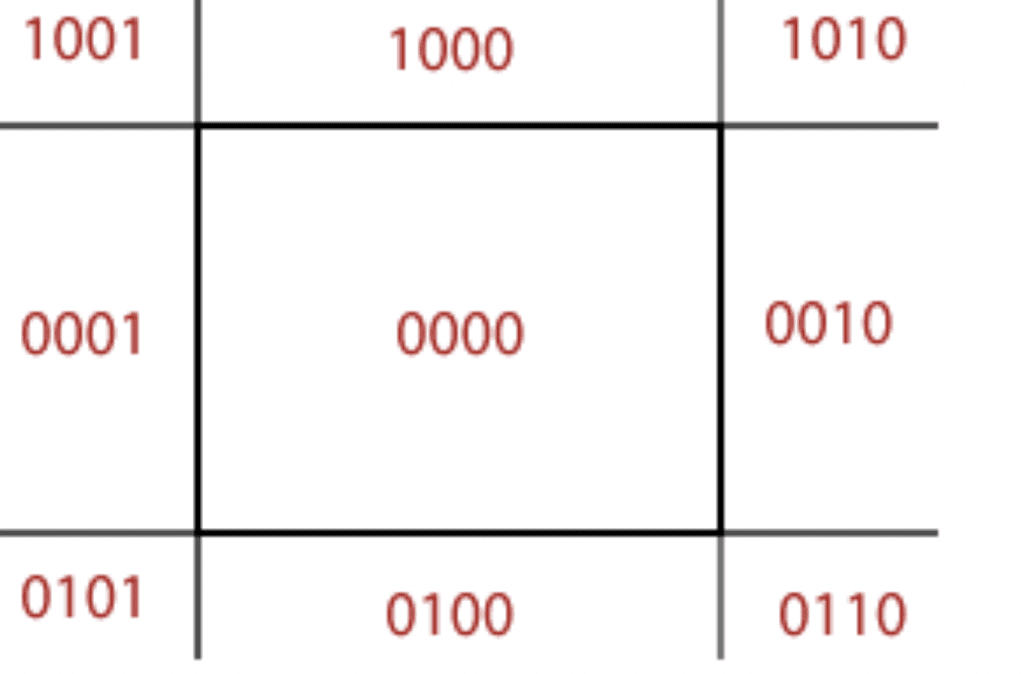

For any line in Cohen Sutherland Line Clipping Algorithm there are three cases possible
- Completely Within the View Port : IF Bitwise OR of region code of two end points of line is 0, as both endpoints will have region code as 0000.
- Completely outside the View Port : Both endpoints share at least one outside region which implies that the line does not cross the visible region. (bitwise AND of endpoints != 0).
- Partially inside the window : Both endpoints are in different regions. In this case, the algorithm finds one of the two points that is outside the rectangular region. The intersection of the line from outside point and rectangular window becomes new corner point and the algorithm repeats
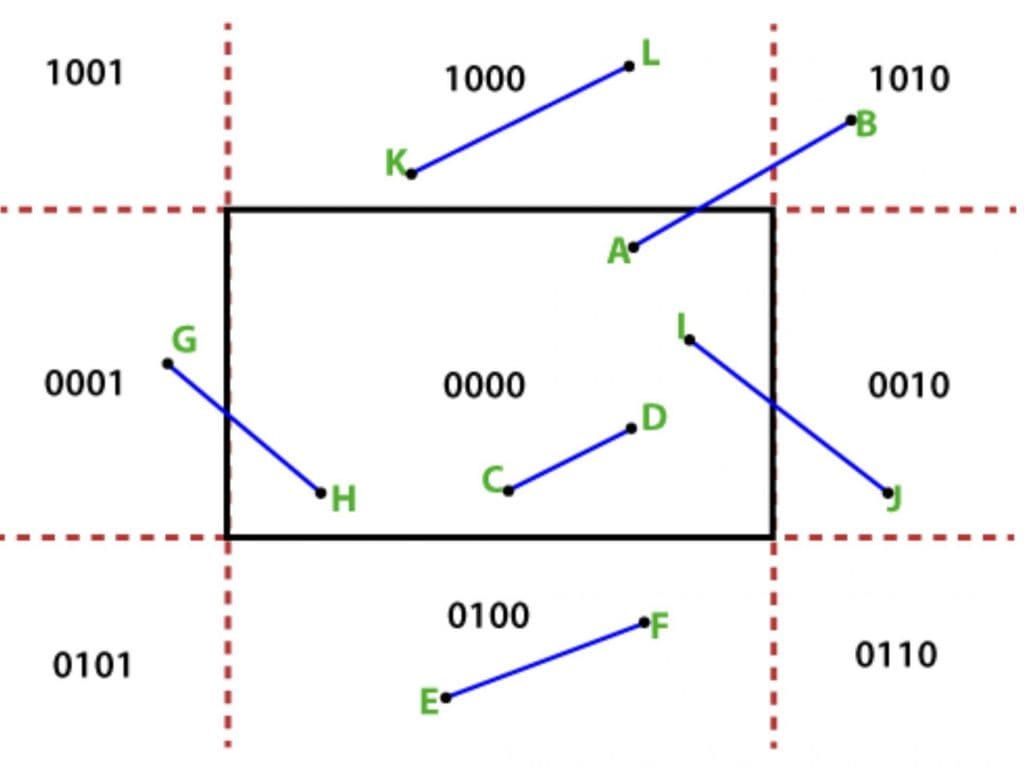

- From above figure we can see line KL is completely outside the RegionCode(K) AND RegionCode(L) !=0
- Similarly Line CD. is completely inside and OR of its region code of endpoints is 0
- For the obvious reasons line GH needs to be clipped.
Let’s look at Pseudocode for Cohen Sutherland Line Clipping Algorithm
1. Assign a region code for two endpoints of given line.
2. Perform OR operation on both endpoints of the line.
IF Result of OR is 0
Then Line is completely within viewport
ELSE
Perform And Operation on both endpoints
IF Result of And is not 0
Then given line is completely outside
ELSE
Clip the line
a. Find intersection points with boundaries using:
m = (y1-y0) (x1-x0)
b. When the line intersects:
Left side boundary of the window port: x = Xmin
Right side boundary of the window port: x = Xmax
Top side boundary of the window port: y = Ymax
Bottom side boundary of the window port: y= Ymin
3. Repeat step 2 until we find a clipped line either trivially accepted or trivially rejected.
4. Repeat step 1 for other linesImplementation
// C++ program to implement Cohen Sutherland Line Clipping Algorithm
#include <iostream>
using namespace std;
// Assigning codes to region
const int INSIDE = 0; // 0000
const int LEFT = 1; // 0001
const int RIGHT = 2; // 0010
const int BOTTOM = 4; // 0100
const int TOP = 8; // 1000
// Defining view port coordinates
const int x_max = 10;
const int y_max = 8;
const int x_min = 4;
const int y_min = 4;
// This Function assign region code for given point(x, y)
int assignRegionCode(double x, double y)
{
int code = INSIDE;
if (x < x_min) // to the left of rectangle
code |= LEFT;
else if (x > x_max) // to the right of rectangle
code |= RIGHT;
if (y < y_min) // below the rectangle
code |= BOTTOM;
else if (y > y_max) // above the rectangle
code |= TOP;
return code;
}
// Cohen Sutherland Line Clipping Algorithm
void cohenSutherlandAlgorithm(double x1, double y1, double x2, double y2)
{
// Assigning region to endpoints of line
int code1 = assignRegionCode(x1, y1);
int code2 = assignRegionCode(x2, y2);
bool accept = false;
// Repeat the process till line is completely outside or inside
while (true) {
// Perform OR on endpoints
if ((code1 | code2 ) ==0) {
// If result is 0 then both endpoints lie within rectangle
accept = true;
break;
}
// Perform And on endpoints
else if (code1 & code2) {
// If result is not zero this means both endpoints are outside rectangle
break;
}
else {
// Line clipping required
int code_out;
double x, y;
// The endpoint which does-not have region code 0000 is outside the view port
if (code1 != 0)
code_out = code1;
else
code_out = code2;
// Find intersection point;
// using formulas y = y1 + slope * (x - x1),
// x = x1 + (1 / slope) * (y - y1)
// Figure out region where endpoint lies
if (code_out & TOP) {
// point is above the clip rectangle
x = x1 + (x2 - x1) * (y_max - y1) / (y2 - y1);
y = y_max;
}
else if (code_out & BOTTOM) {
// point is below the rectangle
x = x1 + (x2 - x1) * (y_min - y1) / (y2 - y1);
y = y_min;
}
else if (code_out & RIGHT) {
// point is to the right of rectangle
y = y1 + (y2 - y1) * (x_max - x1) / (x2 - x1);
x = x_max;
}
else if (code_out & LEFT) {
// point is to the left of rectangle
y = y1 + (y2 - y1) * (x_min - x1) / (x2 - x1);
x = x_min;
}
// Replace point outside rectangle by intersection point
if (code_out == code1) {
x1 = x;
y1 = y;
code1 = assignRegionCode(x1, y1);
}
else {
x2 = x;
y2 = y;
code2 = assignRegionCode(x2, y2);
}
}
}
if (accept) {
cout << "Line accepted from " << x1 << ", "
<< y1 << " to " << x2 << ", " << y2 << endl;
// Here the user can add code to display the rectangle
// along with the accepted (portion of) lines
}
else
cout << "Line rejected" << endl;
}
int main()
{
// Line Clipping using Cohen Sutherland Line Clipping Algorithm
cohenSutherlandAlgorithm(5, 5, 7, 7);
cohenSutherlandAlgorithm(7, 9, 11, 4);
cohenSutherlandAlgorithm(1, 5, 4, 1);
return 0;
}
Complexity
The time and space complexity of Cohen Sutherland Line Clipping Algorithm are:
- Time complexity:
O(n) - Space complexity:
O(1)
Conclusion
In this article we discussed Cohen Sutherland Line Clipping Algorithm and its implementation. We also discussed its c++ code implementation and its space and time complexities
Got a question or just want to chat? Comment below or drop by our forums, where a bunch of the friendliest people you’ll ever run into will be happy to help you out!


