Table of Contents
ToggleProblem Statement
The Jump Game 2 problem states Given an array of non-negative integers where each element represents the maximum number of steps you can take forward from that position. In other words, if you are at index ‘ i ‘, then nums[i] represents that you can jump to any nums[i + j] where:
0 <= j <= nums[i]andi + j < n
Write a program to find the minimum number of jumps required to reach the end of the array (starting from the first element).
Constraints:
- 1 <= nums.length <= 104
- 0 <= nums[i] <= 1000
- It’s guaranteed that you can reach
nums[n - 1].
Example 1:
// Jump Game 2
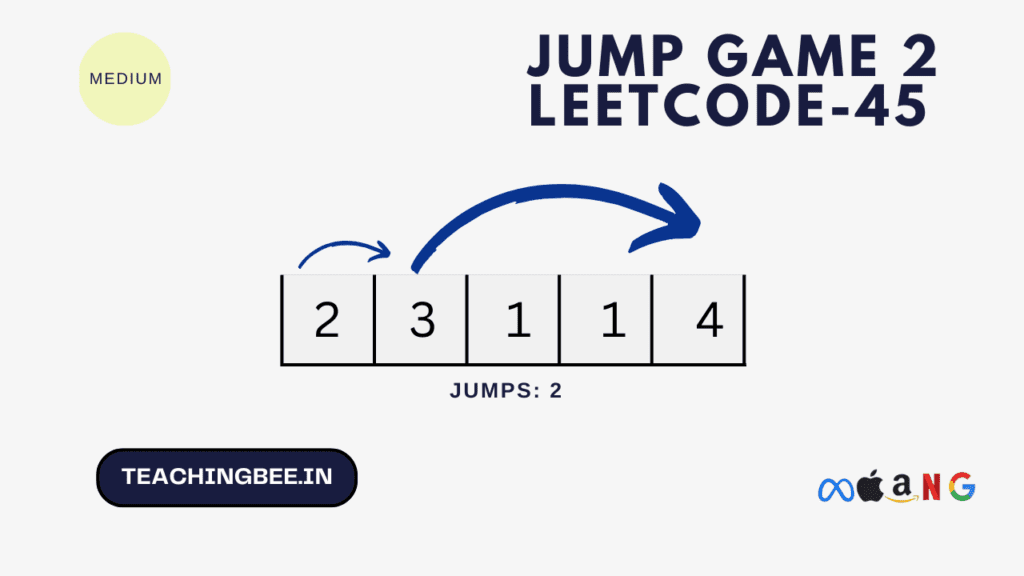
Input: nums = [2,3,1,1,4]
Output: 2Explanation:
Here we start at nums[0] = 2. From this position, the minimum jump we can take is 2 steps. So we jump one step which lands us at index 1 (nums[1] = 3). Then from index 1, the max jump is 3 which takes us to the last index. So the minimum jumps required is 2.
Example 2:
Input: nums = [2,3,0,1,4]
Output: 2Discussed Solutions For Jump Game 2
- Brute Force using recursion
- Dp Solution Memoization
- Dp solution Tabulation
- Greedy Solution (Most optimised)
Recursion (Brute Force)
Intuition
Idea is to explore all possible jump paths from each position in the array and calculate the minimum number of jumps required to reach the end.
Approach
- Base Case:
- If the start index is greater than or equal to the last index of the array, return 0 because no further jumps are needed.
- Recursive Case:
- At each index, you have several choices: you can jump from 1 up to the number at that index.
- For each choice, make a recursive call to find the minimum number of jumps needed from the index you jump to.
- Add 1 to each result (for the jump you just made) and return the minimum of these results.
- Finally, we return the minimum jumps calculated from the starting position (position 0). If it’s still positive infinity, it means there’s no way to reach the end. Otherwise, we return the minimum jumps required.
- Example:
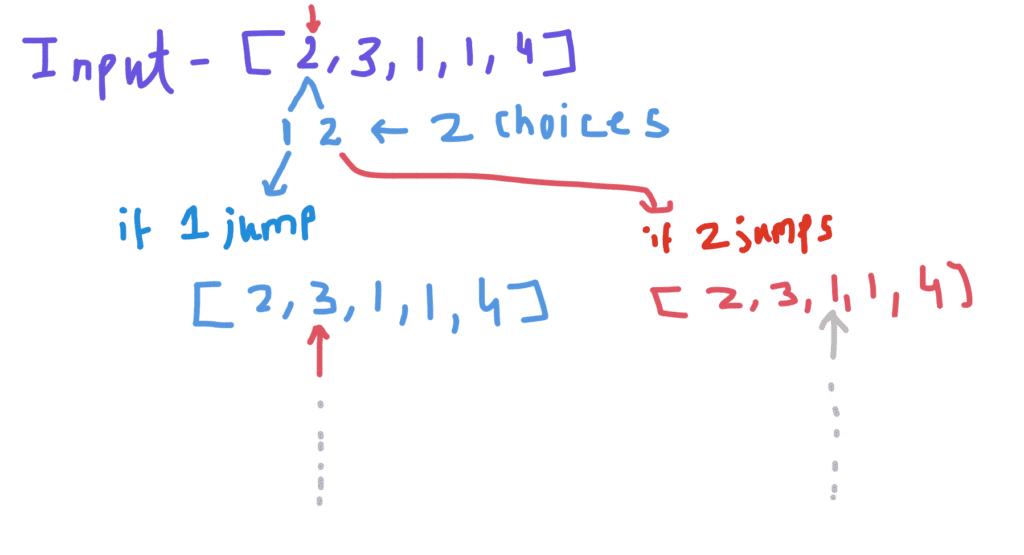
- Consider the array
[2, 3, 1, 1, 4]. - At index 0, you can jump 1 or 2 steps.
- If you jump 1 step, you are at index 1, and you recursively find the minimum number of jumps from there.
- If you jump 2 steps, you are at index 2, and you recursively find the minimum number of jumps from there.
- Return the minimum of the results from the two choices, plus 1 for the jump you just made.
- Consider the array

Code
C++
// C++ Implementation for Jump Game 2
#include <iostream>
#include <vector>
using namespace std;
int jump(vector<int>& nums) {
int n = nums.size();
if (n == 0) return 0;
return jumpRecursive(nums, 0);
}
int jumpRecursive(vector<int>& nums, int position) {
int n = nums.size();
if (position == n - 1) return 0;
if (nums[position] == 0) return INT_MAX;
int minJumps = INT_MAX;
int maxJump = nums[position];
for (int i = 1; i <= maxJump && position + i < n; i++) {
int subJumps = jumpRecursive(nums, position + i);
if (subJumps != INT_MAX) {
minJumps = min(minJumps, 1 + subJumps);
}
}
return minJumps;
}
int main() {
vector<int> nums = {2, 3, 1, 1, 4};
int result = jump(nums);
cout << result << endl; // Output: 2
return 0;
}
Java
// Java Implementation for Jump Game 2
public class JumpGameII {
public int jump(int[] nums) {
if (nums.length == 0) return 0;
return jumpRecursive(nums, 0);
}
private int jumpRecursive(int[] nums, int position) {
int n = nums.length;
if (position == n - 1) return 0;
if (nums[position] == 0) return Integer.MAX_VALUE;
int minJumps = Integer.MAX_VALUE;
int maxJump = nums[position];
for (int i = 1; i <= maxJump && position + i < n; i++) {
int subJumps = jumpRecursive(nums, position + i);
if (subJumps != Integer.MAX_VALUE) {
minJumps = Math.min(minJumps, 1 + subJumps);
}
}
return minJumps;
}
public static void main(String[] args) {
int[] nums = {2, 3, 1, 1, 4};
JumpGameII jumpGame = new JumpGameII();
int result = jumpGame.jump(nums);
System.out.println(result); // Output: 2
}
}
Python
// Python Implementation for Jump Game 2
def jump(nums):
if len(nums) == 0:
return 0
return jumpRecursive(nums, 0)
def jumpRecursive(nums, position):
n = len(nums)
if position == n - 1:
return 0
if nums[position] == 0:
return float('inf')
min_jumps = float('inf')
max_jump = nums[position]
for i in range(1, max_jump + 1):
if position + i < n:
sub_jumps = jumpRecursive(nums, position + i)
if sub_jumps != float('inf'):
min_jumps = min(min_jumps, 1 + sub_jumps)
return min_jumps
nums = [2, 3, 1, 1, 4]
result = jump(nums)
print(result) # Output: 2
JavaScript
// C++ Implementation for Jump Game 2
function jump(nums) {
if (nums.length === 0) return 0;
return jumpRecursive(nums, 0);
}
function jumpRecursive(nums, position) {
const n = nums.length;
if (position === n - 1) return 0;
if (nums[position] === 0) return Infinity;
let minJumps = Infinity;
const maxJump = nums[position];
for (let i = 1; i <= maxJump && position + i < n; i++) {
const subJumps = jumpRecursive(nums, position + i);
if (subJumps !== Infinity) {
minJumps = Math.min(minJumps, 1 + subJumps);
}
}
return minJumps;
}
const nums = [2, 3, 1, 1, 4];
const result = jump(nums);
console.log(result); // Output: 2
Analysis
- The time complexity isO(2^n) or O(n!), that is there are n possible ways to move from an element for each element in the array.
- Space complexity is O(n) – Recursive Call Stack
Dynamic Programming (Memoization)
Intuition
The memoization solution for the Jump Game II problem builds upon the recursive approach by adding a memoization table (also known as a memoization cache) to store and reuse the results of subproblems.
Code
C++
// C++ Implementation for Jump Game 2
#include <iostream>
#include <vector>
using namespace std;
int jump(vector<int>& nums) {
int n = nums.size();
vector<int> memo(n, -1);
memo[0] = 0;
return jumpRecursive(nums, 0, memo);
}
int jumpRecursive(vector<int>& nums, int position, vector<int>& memo) {
if (memo[position] != -1) {
return memo[position];
}
int n = nums.size();
int minJumps = INT_MAX;
int maxJump = nums[position];
for (int i = 1; i <= maxJump && position + i < n; i++) {
int subJumps = jumpRecursive(nums, position + i, memo);
if (subJumps != INT_MAX) {
minJumps = min(minJumps, 1 + subJumps);
}
}
memo[position] = minJumps;
return minJumps;
}
int main() {
vector<int> nums = {2, 3, 1, 1, 4};
int result = jump(nums);
cout << result << endl; // Output: 2
return 0;
}
Java
// Java Implementation for Jump Game 2
public class JumpGameII {
public int jump(int[] nums) {
int n = nums.length;
int[] memo = new int[n];
for (int i = 0; i < n; i++) {
memo[i] = -1;
}
memo[0] = 0;
return jumpRecursive(nums, 0, memo);
}
private int jumpRecursive(int[] nums, int position, int[] memo) {
if (memo[position] != -1) {
return memo[position];
}
int n = nums.length;
int minJumps = Integer.MAX_VALUE;
int maxJump = nums[position];
for (int i = 1; i <= maxJump && position + i < n; i++) {
int subJumps = jumpRecursive(nums, position + i, memo);
if (subJumps != Integer.MAX_VALUE) {
minJumps = Math.min(minJumps, 1 + subJumps);
}
}
memo[position] = minJumps;
return minJumps;
}
public static void main(String[] args) {
int[] nums = {2, 3, 1, 1, 4};
JumpGameII jumpGame = new JumpGameII();
int result = jumpGame.jump(nums);
System.out.println(result); // Output: 2
}
}
Python
// Python Implementation for Jump Game 2
def jump(nums):
n = len(nums)
memo = [-1] * n
memo[0] = 0
return jumpRecursive(nums, 0, memo)
def jumpRecursive(nums, position, memo):
if memo[position] != -1:
return memo[position]
n = len(nums)
min_jumps = float('inf')
max_jump = nums[position]
for i in range(1, max_jump + 1):
if position + i < n:
sub_jumps = jumpRecursive(nums, position + i, memo)
if sub_jumps != float('inf'):
min_jumps = min(min_jumps, 1 + sub_jumps)
memo[position] = min_jumps
return min_jumps
nums = [2, 3, 1, 1, 4]
result = jump(nums)
print(result) # Output: 2
Javascript
// JavaScript Implementation for Jump Game 2
function jump(nums) {
const n = nums.length;
const memo = new Array(n).fill(-1);
memo[0] = 0;
return jumpRecursive(nums, 0, memo);
}
function jumpRecursive(nums, position, memo) {
if (memo[position] !== -1) {
return memo[position];
}
const n = nums.length;
let minJumps = Infinity;
const maxJump = nums[position];
for (let i = 1; i <= maxJump && position + i < n; i++) {
const subJumps = jumpRecursive(nums, position + i, memo);
if (subJumps !== Infinity) {
minJumps = Math.min(minJumps, 1 + subJumps);
}
}
memo[position] = minJumps;
return minJumps;
}
const nums = [2, 3, 1, 1, 4];
const result = jump(nums);
console.log(result); // Output: 2
Analysis
- The time complexity is O(n^2) or O(n^3)
- Space complexity is O(n) – Memoization Table
Dynamic Programming (Tabulation)
Intuition
Like in memoization solution, we can break it down into smaller subproblems. The minimum jumps needed to reach a particular position depend on the minimum jumps needed to reach previous positions.The tabulation solution takes a bottom-up approach, starting from the beginning of the array and gradually building up the solution by considering the minimum jumps needed to reach each position. The table is initialized with a large value (e.g., infinity) except for the first position, which is initialized to 0 because it takes 0 jumps to reach itself.
Approach
We iterate through the positions in the array from left to right. For each position, we consider all possible jumps from the previous positions and update the minimum jumps required to reach the current position. After processing all positions, the value at the last position of the dynamic programming table represents the minimum jumps needed to reach the end of the array.
Code
C++
// C++ Implementation for Jump Game 2
#include <iostream>
#include <vector>
#include <climits>
using namespace std;
int jump(vector<int>& nums) {
int n = nums.size();
vector<int> dp(n, INT_MAX);
dp[0] = 0; // It takes 0 jumps to reach the starting position.
for (int i = 0; i < n; i++) {
for (int j = 1; j <= nums[i] && i + j < n; j++) {
dp[i + j] = min(dp[i + j], dp[i] + 1);
}
}
return dp[n - 1];
}
int main() {
vector<int> nums = {2, 3, 1, 1, 4};
int result = jump(nums);
cout << result << endl; // Output: 2
return 0;
}
Java
// Java Implementation for Jump Game 2
public class JumpGameII {
public int jump(int[] nums) {
int n = nums.length;
int[] dp = new int[n];
Arrays.fill(dp, Integer.MAX_VALUE);
dp[0] = 0; // It takes 0 jumps to reach the starting position.
for (int i = 0; i < n; i++) {
for (int j = 1; j <= nums[i] && i + j < n; j++) {
dp[i + j] = Math.min(dp[i + j], dp[i] + 1);
}
}
return dp[n - 1];
}
public static void main(String[] args) {
int[] nums = {2, 3, 1, 1, 4};
JumpGameII jumpGame = new JumpGameII();
int result = jumpGame.jump(nums);
System.out.println(result); // Output: 2
}
}
Python
// Python Implementation for Jump Game 2
def jump(nums):
n = len(nums)
dp = [float('inf')] * n
dp[0] = 0 # It takes 0 jumps to reach the starting position.
for i in range(n):
for j in range(1, nums[i] + 1):
if i + j < n:
dp[i + j] = min(dp[i + j], dp[i] + 1)
return dp[-1]
nums = [2, 3, 1, 1, 4]
result = jump(nums)
print(result) # Output: 2
Javascript
// JavaScript Implementation for Jump Game 2
function jump(nums) {
const n = nums.length;
const dp = new Array(n).fill(Infinity);
dp[0] = 0; // It takes 0 jumps to reach the starting position.
for (let i = 0; i < n; i++) {
for (let j = 1; j <= nums[i] && i + j < n; j++) {
dp[i + j] = Math.min(dp[i + j], dp[i] + 1);
}
}
return dp[n - 1];
}
const nums = [2, 3, 1, 1, 4];
const result = jump(nums);
console.log(result); // Output: 2
Analysis
- The time complexity is O(n^2) or O(n^3)
- Space complexity is O(n) – DP Table
Greedy
Intuition
The intuition behind this algorithm is to use a greedy approach to determine the minimum number of jumps required.
At each position, we calculate the farthest index we can reach from that position and update max_reach accordingly. When we reach the point where i is equal to max_reach, it means we need to make a jump to reach the farthest possible index with the current number of jumps.
Approach
Initialize two variables: max_reach and steps. Set max_reach to 0 and steps to 0. max_reach represents the maximum index that can be reached with the current number of jumps, and steps represents the minimum number of jumps needed to reach the end.Iterate through the nums array from index 0 to len(nums) - 2 (the last index is excluded since we've already reached it if we're there).At each position i, update max_reach to be the maximum of its current value and i + nums[i]. This represents the farthest index reachable from the current position i.If i is equal to the current max_reach, it means we need to make a jump. Increment steps by 1 and update max_reach to the farthest index we can reach with the current number of jumps.Continue iterating through the array until you reach the last index.Return the steps as the minimum number of jumps needed to reach the end.
Code
C++
// C++ Implementation for Jump Game 2
#include <iostream>
#include <vector>
using namespace std;
int jump(vector<int>& nums) {
int max_reach = 0;
int steps = 0;
int current_max_reach = 0;
for (int i = 0; i < nums.size() - 1; i++) {
current_max_reach = max(current_max_reach, i + nums[i]);
if (i == max_reach) {
max_reach = current_max_reach;
steps++;
}
}
return steps;
}
int main() {
vector<int> nums = {2, 3, 1, 1, 4};
int result = jump(nums);
cout << result << endl; // Output: 2
return 0;
}Java
// Java Implementation for Jump Game 2
public class JumpGameII {
public static int jump(int[] nums) {
int maxReach = 0;
int steps = 0;
int currentMaxReach = 0;
for (int i = 0; i < nums.length - 1; i++) {
currentMaxReach = Math.max(currentMaxReach, i + nums[i]);
if (i == maxReach) {
maxReach = currentMaxReach;
steps++;
}
}
return steps;
}
public static void main(String[] args) {
int[] nums = {2, 3, 1, 1, 4};
int result = jump(nums);
System.out.println(result); // Output: 2
}
}Python
// Python Implementation for Jump Game 2
def jump(nums):
max_reach = 0
steps = 0
current_max_reach = 0
for i in range(len(nums) - 1):
current_max_reach = max(current_max_reach, i + nums[i])
if i == max_reach:
max_reach = current_max_reach
steps += 1
return steps
nums = [2, 3, 1, 1, 4]
result = jump(nums)
print(result) # Output: 2
Javascript
// JavaScript Implementation for Jump Game 2
function jump(nums) {
let maxReach = 0;
let steps = 0;
let currentMaxReach = 0;
for (let i = 0; i < nums.length - 1; i++) {
currentMaxReach = Math.max(currentMaxReach, i + nums[i]);
if (i === maxReach) {
maxReach = currentMaxReach;
steps++;
}
}
return steps;
}
const nums = [2, 3, 1, 1, 4];
const result = jump(nums);
console.log(result); // Output: 2
Dry Run
Let’s dry run this algorithm by taking an example:
Consider the input array nums = [2, 3, 1, 1, 4].
Let’s go step by step through the algorithm:
- Initialize
max_reachto 0 andstepsto 0.max_reach= 0steps= 0
- Iteration 1 (i = 0): Start iterating through the array:
i= 0max_reach= max(0, 0 + 2) = 2- Since
iis equal tomax_reach, we need to make a jump. - Increment
stepsby 1. steps= 1
- Iteration 2 (i = 1):
i= 1max_reach= max(2, 1 + 3) = 4- Since
iis not equal tomax_reach, we don’t need to make a jump.
- Iteration 3 (i = 2):
i= 2max_reach= max(4, 2 + 1) = 4- Since
iis not equal tomax_reach, we don’t need to make a jump.
- Iteration 4 (i = 3):
i= 3max_reach= max(4, 3 + 1) = 4- Since
iis not equal tomax_reach, we don’t need to make a jump.
- Iteration 5 (i = 4):
i= 4max_reach= max(4, 4 + 4) = 8- Since
iis equal tomax_reach, we need to make a jump. - Increment
stepsby 1. steps= 2
- Since we’ve reached the end. We don’t need to make any more jumps.
- Return
steps, which is 2.
Analysis
- The time complexity is Typically Linear (O(n log n) or O(n))
- Space complexity is O(1) – Constant
Complexities For Different Jump Game 2 Solutions
| Approach | Time Complexity | Space Complexity |
|---|---|---|
| Recursive Brute Force | Exponential (e.g., O(2^n) or O(n!)) | O(n) – Recursive Call Stack |
| Memoization (DP) | Polynomial (e.g., O(n^2) or O(n^3)) | O(n) – Memoization Table |
| Tabulation (DP) | Polynomial (e.g., O(n^2) or O(n^3)) | O(n) – DP Table |
| Greedy | Typically Linear (O(n log n) or O(n)) | O(1) – Constant |
Try out our free resume checker service where our Industry Experts will help you by providing resume score based on the key criteria that recruiters and hiring managers are looking for.