Table of Contents
ToggleDistance vector routing is a distributed iterative algorithm used by routers to determine optimal paths to destinations on computer networks. In this article we will see how the distance vector routing algorithm works.We will also see step-by-step process routers follow to exchange routing information and converge on the most efficient routes.
What is distance vector routing in networking?
Distance Vector Routing Algorithm is based on the Bellman-Ford algorithm and is used to determine the optimal path for data packets in a computer network. The algorithm is iterative and involves routers exchanging information about their routing tables to converge on the most efficient routes.
How Does Distance Vector Routing Algorithm Work?
The Distance Vector Routing (DVR) algorithm involves several steps that routers follow to exchange information and determine the best paths to reach destinations. Here are the key steps involved in Distance Vector Routing:
- Initialisation
- Exchange of Distance Vectors
- Vector Update
- Iterative Process
- Convergence
- Routing Table Update
- Periodic Updates
Step 1: Initialisation
Each router initialises its own distance vector (Dx(y)). Initially, it knows the cost to reach itself (Dx(x)=0) and also knows the cost to reach to its neighbours. The cost to reach other non neighbour routers are marked as infinity ( Dx(y) = ∞ for y ≠ x where y is non neighbour)
Here Dx(y) is the cost from router x to destination y.
Step 2: Exchange of Distance Vectors
Routers periodically share their distance vectors with their neighbours. This information includes the cost to reach each destination as well as the path taken to reach those destinations.
Step 3: Vector Update
Upon receiving a neighbour’s distance vector, a router updates its own distance vector using the Bellman-Ford update formula.
Dx(y)=min(Dx(y),Dx(z)+Dz(y))where:
- Dx(y) is the cost from router x to destination y.
- Dx(z) is the cost from router x to the neighbour z.
- Dz(y) is the cost from neighbour z to destination y.
This formula helps the router consider the minimum cost path to reach each destination.
Step 4: Iterative Process
Steps 2 and 3 are repeated iteratively. Routers continue to exchange and update their distance vectors. This iterative process helps routers converge toward a consistent and accurate view of the network.
Step 5: Convergence
The process continues until all routers have consistent and up-to-date distance vectors. This state is known as convergence. It occurs when routers no longer need to update their distance vectors.
At this point, routers have a stable understanding of the network topology and the best paths to reach each destination.
Step 6: Routing Table Update
Based on the converged distance vectors, each router updates its routing table. The routing table contains information about the next hop for each destination, along with the associated cost.
Step 7: Periodic Updates
Even in the absence of topology changes, routers continue to exchange their distance vectors periodically. Steps 2 to 6 are repeated at regular intervals to ensure the routing information stays up-to-date.
This ensures that routers stay informed about the state of the network and can quickly adapt to any changes that may occur.
Adaptation to Network Changes
If there is a change in the network, such as a link going down or coming up, routers detect the change through the periodic updates. They then update their distance vectors accordingly, and the iterative process resumes until convergence is reached.
The Distance Vector Routing algorithm is designed to dynamically adapt to changes in the network topology. This ensures that routers can quickly respond to additions, removals, or modifications of network links.
Routers make forwarding decisions based on their routing tables. The path chosen is the one with the minimum cost, where the cost is typically measured in terms of metrics like hop count, bandwidth, or delay.
Example of Distance Vector Routing Algorithm
Let’s understand the above DVR steps with example. Consider below network topology.
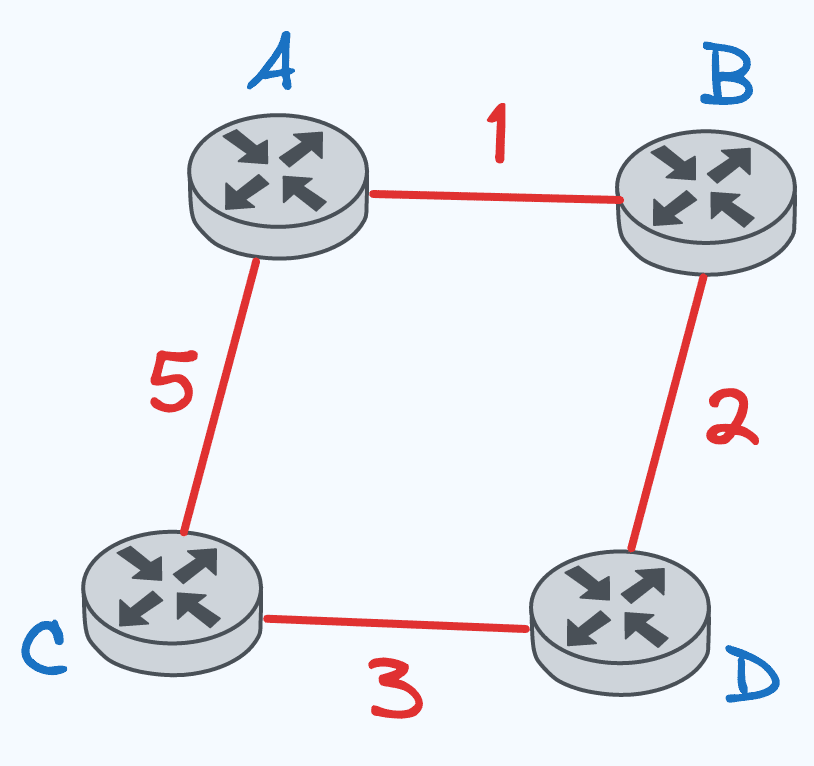

Step 1: Initialization
Initially, each router sets its distance vector and sets infinity for non neighbour destinations. The distance to itself is always 0. For example for Router A, B and C are neighbours where as D is non neighbour. So initial routing table for A will look like
Router A:
| Destination | Next Hop | Cost |
|---|---|---|
| A | – | 0 |
| B | – | 1 |
| C | – | 5 |
| D | – | ∞ |
- Similary, Router B, C, D will have similiar values filled in initial tables.
Initial Distance Vectors
- Router A: {‘A’: 0, ‘B’: 1, ‘C’: 5, ‘D’:
∞} - Router B: {‘A’: 1, ‘B’: 0, ‘C’:
∞‘D’: 2} - Router C: {‘A’: 5, ‘B’:
∞, ‘C’: 0, ‘D’: 3} - Router D: {‘A’:
∞, ‘B’: 2, ‘C’: 3, ‘D’: 0}
Step 2: Exchange of Distance Vectors
Router A sends its distance vector to neighbours B and C.
Similarly, Router B will exchange its distance vector with neighbours A and D.
Router C with neighbours A and D
And, Router D with neighbours B and C
Distance vector from A: [0, 1, 5, ∞]Step 3: Vector Update
- Router B receives from A:
[0, 1, 5, ∞]and D: [∞, 2 , 3 , 0] - Router B updates its distance vector using only these two distance vector received from neighbours using the Bellman-Ford equation.
Cost(B, A) = min(Cost(B,A)+ Cost(A,A) , Cost(B,D) + Cost(D,A), Cost(B,A))
= min(1 + 0, 2 + ∞, 1) = 1
Cost(B, C) = min(Cost(B,A)+ Cost(A,C) , Cost(B,D) + Cost(D,C), Cost(B, C))
= min(1 + 5, 2 + 3, ∞) = 5
Cost(B, D) = min(Cost(B,A)+ Cost(A,D) , Cost(B,D) + Cost(D,D), Cost(B, D))
= min(1 + ∞, 2 + 0, 2) = 2So, new Distance vector will become B: [1, 0, 5, 2]
Router C and D update their vectors similarly.
Note: To update distance vector Router will only use distance vector of its neighbours and will broadcast its distance vector to only its neighbour
Step 4: Iterative Process
After the first iteration, the new distance vectors are:
- Router A:
[0, 1, 5, ∞] - Router B:
[1, 0, 5, 2] - Router C:
[5, 5, 0, 3] - Router D:
[3, 2, 3, 0]
Step 5: Convergence
The vectors have still not converged, so another iteration is needed.
Step 3: Vector Update – Iteration 2:
- Router A receives from B:
[1, 0, 5, 2]and C:[5, 5, 0, 3] - Router A updates its distance vector:
Cost(A, B) = min(Cost(A,B)+ Cost(B,B) , Cost(A,C) + Cost(C,B), Cost(A, B))
= min(1 + 0, 5 + 5, 1) = 1
Cost(A, C) = min(Cost(A,B)+ Cost(B,C) , Cost(A,C) + Cost(C,C), Cost(A, C))
= min(1 + 5, 5 + 0, 5) = 5
Cost(A, D) = min(Cost(A,B)+ Cost(B,D) , Cost(A,C) + Cost(C,D), Cost(A, D))
= min(1 + 2, 5 + 3, ∞) = 3- Similarly, other routers update their vectors.
Step 4: Iterative Process – After Iteration 2:
After the second iteration, the new distance vectors are:
Router A: [0, 1, 5, 3]
Router B: [1, 0, 5, 2]
Router C: [5, 6, 0, 4]
Router D: [3, 2, 4, 0]
Step 6: Routing Table Update
The vectors converge after 2 iterations. Routing tables are updated based on the converged distance vectors.The routing tables now contain the least cost path to each destination discovered by the distance vector algorithm. Final tables looks like:
Router A:
| Destination | Next Hop | Cost |
|---|---|---|
| A | – | 0 |
| B | B | 1 |
| C | A | 5 |
| D | B | 3 |
Router B:
| Destination | Next Hop | Cost |
|---|---|---|
| A | A | 1 |
| B | – | 0 |
| C | D | 5 |
| D | D | 2 |
Router C:
| Destination | Next Hop | Cost |
|---|---|---|
| A | A | 5 |
| B | D | 5 |
| C | – | 0 |
| D | D | 3 |
Router D:
| Destination | Next Hop | Cost |
|---|---|---|
| A | B | 3 |
| B | B | 2 |
| C | C | 3 |
| D | – | 0 |
These tables represent the final state of the routing tables after convergence in the Distance Vector Routing algorithm.
Count to infinity problem in Distance Vector routing
The “count to infinity” problem is a scenario in Distance Vector routing algorithm where routers in a network may incorrectly believe they can reach a destination through a longer path with a lower cost.
This leads to a loop in the routing information and potentially infinite costs being associated with routes. It typically arises when there’s a failure in the network, and routers take time to recognize the failure and update their routing tables.
Resolution
To address the count to infinity problem, several techniques are employed:
- Split Horizon: Routers avoid sending information about routes back to the neighbor from which they learned about the route. This prevents the propagation of incorrect information.
- Route Poisoning: When a router determines that a route is unreachable, it immediately advertises this information to its neighbours, ensuring rapid dissemination of the failure.
- Hold-Down Timers: Introduce timers to prevent rapid and continuous updates. During a hold-down period, a router refrains from accepting updates for a route. This helps stabilize the network and prevents the propagation of incorrect information during transient states.
By combining these techniques, the count to infinity problem is mitigated, and the routing algorithms achieve faster convergence and increased stability in the face of network changes.
Types Of Distance Vector Routing
Different types of Vector Routing Protocol are
- Routing Information Protocol (RIP)
- Border Gateway Protocol (BGP)
- Enhanced Interior Gateway Routing Protocol (EIGRP)
- Routing Table Protocol (RTP)
- AppleTalk Routing Table Protocol (AURP)
Routing Information Protocol (RIP):
RIP is a widely utilized Distance Vector Routing (DVR) protocol, employing hop count as its primary metric. With a maximum hop limit of 15, RIP initiates periodic route updates every 30 seconds, making it a straightforward yet effective routing protocol.
Border Gateway Protocol (BGP):
As an interdomain routing protocol operating between autonomous systems, BGP stands out with its path vector approach—a variant of distance vector. Unlike traditional metrics, BGP relies on policy-based path selections, and updates are triggered by routing changes, departing from periodic intervals.
Enhanced Interior Gateway Routing Protocol (EIGRP):
Developed by Cisco, EIGRP is an advanced DVR protocol that employs composite metrics such as bandwidth, delay, and reliability. Its incremental updates, which convey only changes, contribute to efficient network operation, and the protocol achieves fast convergence through the Diffusing Update Algorithm (DUAL).
Routing Table Protocol (RTP):
RTP, an obsolete DVR protocol integrated into the OSI protocol stack, utilized delay as a routing metric. Over time, it has been largely replaced by more modern and robust routing protocols like OSPF.
AppleTalk Routing Table Protocol (AURP):
AURP, a proprietary Apple protocol, is specifically designed for routing between AppleTalk networks. Operating on principles akin to distance vector protocols, it addresses the routing needs within the Apple ecosystem.
Advantages Of Distance Vector Routing
The main advantages of the Distance Vector Routing (DVR) algorithm are
Simplicity
- Very simple and easy to configure
- Each router only needs to inform directly connected neighbors
- No complex topology tracking required
Low processing and resource overhead
- Only periodic small updates sent between routers
- Tables do not grow large since infos only about least cost routes
- Minimal memory and computing needed to exchange and process updates
Distributed operation
- No dependency on a central router for path info
- If one router fails, neighbours automatically try alternates
- Reliable since processing is distributed across routers
Works well in small homogeneous networks
- Converges fast for small uniform topologies
- Easy migration from basic network setups
Disadvantages Of Distance Vector Routing
The main advantages of the Distance Vector Routing (DVR) algorithm are
Slow convergence on larger networks
- Count to infinity problem leads to slower convergence
- Routing loops can occur or suboptimal routes selected
- Larger and more complex topologies take longer to stabilize
Lack of comprehensive network view
- Routers have information only about directly connected routes
- No end to end visibility of overall network topology state
Route flapping
- Periodic broadcast of vectors consumes bandwidth
- Events like link failure trigger flooding of updates
Simplistic metrics
- Limited metrics like hop count do not reflect actual throughput
- Advanced metrics like latency and jitter not available
In summary, DVR works very well for small networks but has limitations in handling scale and speed – key considerations for real world service provider environments.
Key Takeaways
- Distance vector routing involves routers initializing routing tables and then periodically sharing these tables with neighbors
- Routers use the Bellman-Ford formula to update their routing tables based on cost information received from neighbours
- An iterative process of exchange and vector updates occurs until routing tables become stable or converge
- Converged routing tables contain the least cost paths to each destination learned dynamically
- The algorithm adapts to changes in network conditions through regular routing updates
- Techniques like split horizon and hold-down timers prevent issues like routing loops
- Types of distance vector protocols include RIP, BGP, EIGRP each with specific features
- Main advantages are simplicity and low overhead, disadvantages relate to scalability
You may also like
Checkout more Algorithms here.
I hope You liked the post 👍. For more such posts, 📫 subscribe to our newsletter. Try out our free resume checker service where our Industry Experts will help you by providing resume score based on the key criteria that recruiters and hiring managers are looking for.
FAQ
Is OSPF distance vector routing?
No, OSPF (Open Shortest Path First) is not a distance vector routing protocol. OSPF is categorized as a link-state routing protocol. In OSPF, routers exchange information about the state of their links and use this information to build a detailed and accurate representation of the network’s topology.
This contrasts with distance vector protocols, where routers share information about distances or costs to reach other routers. OSPF’s link-state approach allows for faster convergence, more efficient use of network resources, and scalability in larger networks.
What is distance sequenced distance-vector routing?
Distance Sequenced Distance-Vector Routing (DSDV) is a proactive routing protocol designed for wireless ad-hoc networks. It utilises a table-driven approach where each node maintains a routing table containing sequences to determine the most recent information. DSDV aims to provide a loop-free and stable routing environment by incorporating sequence numbers to differentiate between old and updated routing information.
DSDV (Destination-Sequenced Distance Vector) and DVR (Distance Vector Routing) are both routing protocols, but they have significant differences in terms of their operation and characteristics.
DSDV (Destination-Sequenced Distance Vector) is a proactive routing protocol using sequence numbers for loop prevention, designed for wireless ad-hoc networks. DVR (Distance Vector Routing) is a broader term, encompassing both proactive (e.g., RIP) and reactive (e.g., AODV) routing protocols.
How is DVR different from LSR?
Distance Vector Routing and Link State Routing are two fundamental approaches to routing. In DVR, routers share information about distances to other routers, and updates are based on the Bellman-Ford equation. It is simpler but can be prone to slow convergence.
In contrast, Link State Routing protocols, like OSPF, involve routers sharing information about the state of their links. This approach allows for a more accurate representation of the network’s topology, faster convergence, and efficient use of network resources.