Program To Print Sum Of All Cubes In Java Between 1 To N

Finding the sum of consecutive cube numbers is a common problem in programming. In this article, we will look at techniques for calculating sum of all cubes in Java Between 1 to n.

Problem Statement

Given a number n, print sum of all cubes in java between 1 to n.

Examples:

Input: 3

Output: 36

Explanation

Cubes of first three natural numbers is 1^3 + 2^3 + 3^3 =36.

Print Sum Of All Cubes In Java Solution

We will discuss two solutions here:

1. Naive Approach Using Loops
2. Using Mathematical Formula

Naive Approach

The idea here is to iterate from 1 to n using loop and add the cube of current number to the sum.

Java Code Implementation

Let’s see Java Program for cube sum of first n natural numbers using Naive Approach

// Java Program for cube sum of first n natural numbers using Naive Approach

public class SumOfCubes {

    // Method to calculate the sum of cubes of natural numbers up to n
    public static long sumOfCubes(int n) {
        long sum = 0; // Initialize sum to 0
        for (int i = 1; i <= n; i++) {
            sum += i * i * i; // Add the cube of the current number to the sum
        }
        return sum; // Return the computed sum
    }

    public static void main(String[] args) {
        int n = 3; // Example input
        long result = sumOfCubes(n); // Calculate the sum of cubes
        System.out.println("The sum of cubes of first " + n + " natural numbers is: " + result);
    }
}

Output:

The sum of cubes of first 3 natural numbers is: 36

Time Complexity: O(n).

This is because we have to loop through each number from 1 to n and perform a constant-time operation (cubing a number and adding it to the sum).

Space Complexity: O(1).

Using Mathematical Formula

Mathematical Formula to get sum of cube of first n natural number is

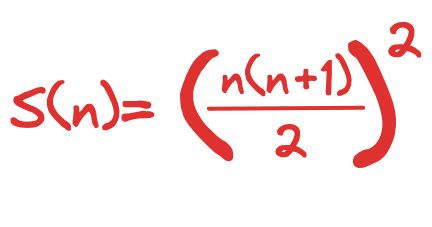
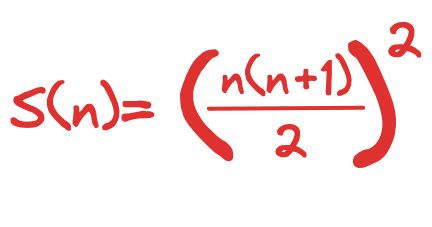
To know the proof and derivation of this formula check out this article. We will use this formula to calculate sum of cubes of numbers between 1 to n.

Java Code Implementation

Let’s see Java Program for cube sum of first n natural numbers using Mathematical Formula

// Sum of cube of first n natural number in java using formula

public class SumOfCubes {

    // Function to calculate the sum of cubes of the first n natural numbers
    public static long sumOfCubes(int n) {
        long sum = (long) n * (n + 1) / 2;  // Sum of the first n natural numbers
        sum *= sum;  // Squaring the sum to get the sum of cubes
        return sum;
    }

    public static void main(String[] args) {
        int n = 5;  // Example input
        System.out.println("The sum of cubes of the first " + n + " natural numbers is: " + sumOfCubes(n));
    }
}

Output:

The sum of cubes of the first 5 natural numbers is: 225

Time Complexity: O(1).

This is because the calculations are done in constant time. No matter the size of n, the computational steps remain the same

Space Complexity: O(1).

Key Takeaways

• A naive iterative approach uses a loop to cube each number and add to the sum
• Mathematical formulas can calculate the sum in constant time without loops
• Time complexity is O(n) for iteration vs O(1) for the formula
• Understanding both methods provides a good overview of algorithmic approaches

Similar Posts

Add Days To The Current Date in Java

Calculate Area of Hexagon in Java

Program to Calculate EMI in Java

Calculate Area of a Circle in Java

Leap Year Program In Java

Checkout more Java Tutorials here.

I hope You liked the post ?. For more such posts, ? subscribe to our newsletter. Try out our free resume checker service where our Industry Experts will help you by providing resume score based on the key criteria that recruiters and hiring managers are looking for.

FAQ