Table of Contents
ToggleWhat is Recursion in C?
Recursion in C is a technique where a function calls itself. This allows the function to repeat the same logic over and over, just on smaller pieces of the problem.
Recursion in C requires two things:
- A base case that stops the recursion. This is the simplest version of the problem.
- A recursive step that calls the function again.
With each call, the problem becomes simpler until you reach the base case. This allows elegant solutions for problems like traversing trees or calculating factorials. However, recursion can lead to infinite loops if not written carefully. It also requires more memory since each call adds to the stack. Overall, recursion is a powerful technique for repeating logic by reducing problems to simpler versions of themselves.
In this article, we will learn recursion in C its working, examples and applications.
Base case:
This is the simplest case where the function does not call itself but returns a value directly. The base case is essential to prevent infinite recursion.
Recursive call
This is where the function calls itself with a modified argument to reduce the problem toward the base case.
For Example: Below is Recursive function In C to calculate sum of n natural numbers.
#include <stdio.h>
// Recursive function to calculate the sum of the first n natural numbers
int sumOfNaturalNumbers(int n) {
// Base case
if (n == 0) {
return 0; // Sum of no numbers is 0
} else {
// Recursive call
return n + sumOfNaturalNumbers(n - 1);
}
}
int main() {
// Example: Calculate the sum of the first 5 natural numbers
int result = sumOfNaturalNumbers(5);
printf("Sum of the first 5 natural numbers: %d\n", result);
return 0;
}
In above code
- Base Case:
- The base case is when n is 0. In this case, the function returns 0 as the sum of no numbers is 0.
- Recursive Call:
- If n is not 0, the function calls itself with n−1.
- Recursive Call Highlight:
return n + sumOfNaturalNumbers(n - 1);
How does Recursion in C work?
Recursion is when a function calls itself. This allows the function to repeat and break a big problem down into smaller steps. Each function call creates a distinct stack frame in memory, holding information like local variables, parameters, and return addresses. As the recursion progresses, the program checks for a base case. When the base case is equals true, the function returns and quits; otherwise, the recursive case is executed. During unwinding, each stack frame is removed one by one, and the program returns to the previous point of execution.
So recursion in C works by:
- Having a base case to stop recursion
- Having a recursive case that calls the function on smaller inputs
- Unwinding the stack once the base case is reached
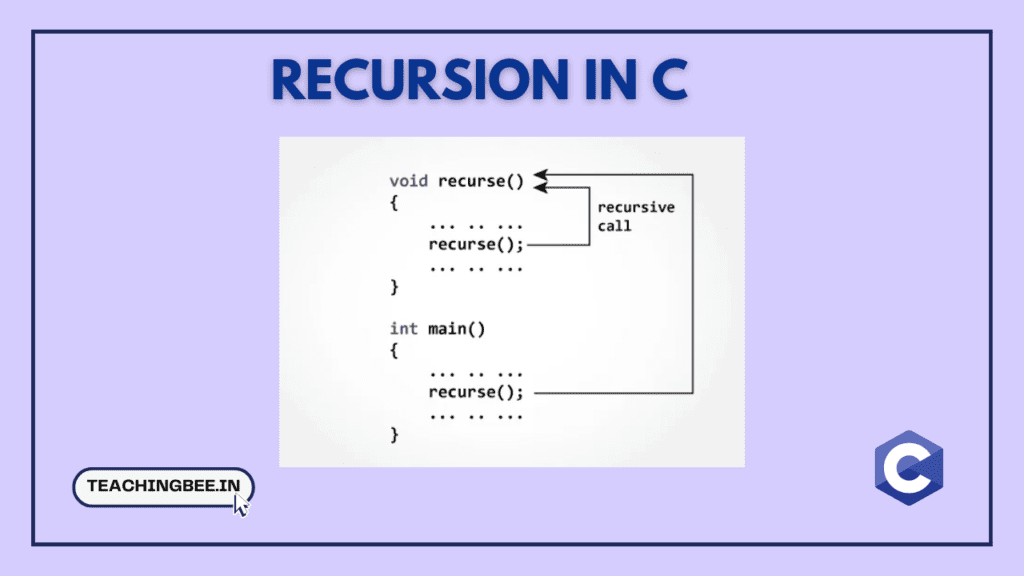
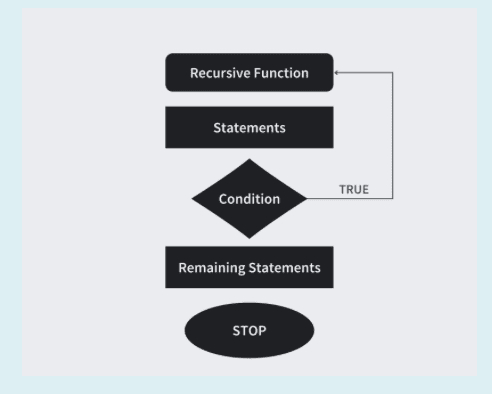
The following image shows a recursive function with a recursive call inside that function, which calls the recursive function until the condition of the problem is satisfied. The program control then goes for the remaining statements and stops it when the condition is satisfied.

For example let’s see recursive calculation of factorial, where the base case is when the input is 0 or 1. The recursive calls then unfold, and as the base case is reached, the stack unwinds, allowing the final result to be computed.
In below program
Execution Steps:
factorial(5)is called, a stack frame is added.factorial(4)is called within the function, a new stack frame is added.- This process continues until
factorial(1)is called. factorial(1)is the base case, the stack starts unwinding.- As the stack unwinds, the factorial is calculated at each step.
#include <stdio.h>
int factorial(int n) {
// Base case
if (n == 0 || n == 1) {
return 1;
}
// Recursive call
return n * factorial(n - 1);
}
int main() {
int result = factorial(5); // Example: Calculate factorial of 5
printf("Factorial of 5 is: %d\n", result);
return 0;
}
Examples of the Recursion in C
Let’s look into some examples of Recursion in C:
1. C Program To Calculate Factorial using Recursion
C Program:
#include <stdio.h>
int factorial(int n) {
// Base case
if (n == 0 || n == 1) {
return 1;
}
// Recursive call
return n * factorial(n - 1);
}
int main() {
int result = factorial(5); // Example: Calculate factorial of 5
printf("Factorial of 5 is: %d\n", result);
return 0;
} Output:
Factorial of 5 is: 120The program uses recursion to calculate the factorial of a number (in this case, 5). The recursive function multiplies the current number with the factorial of the number one less than itself until the base case (n = 0 or n = 1) is reached.
2. C Program To Print Fibonacci Series Using Recursion
C Program:
#include <stdio.h>
int fibonacci(int n) {
// Base case
if (n <= 1) {
return n;
}
// Recursive call
return fibonacci(n - 1) + fibonacci(n - 2);
}
int main() {
for (int i = 0; i < 6; ++i) {
printf("%d ", fibonacci(i));
}
return 0;
} Output:
0 1 1 2 3 5The program uses recursion to generate the Fibonacci series. The recursive function adds the two preceding numbers in the series until the base case (n <= 1) is reached.
3. C Program for Tower of Hanoi Using Recursion
The Tower of Hanoi is a classic problem that involves moving a stack of disks from one pole to another, with the constraint that only one disk can be moved at a time, and a larger disk cannot be placed on top of a smaller one. The program consists of two main parts:
C Program:
#include <stdio.h>
void towerOfHanoi(int n, char source, char auxiliary, char destination) {
// Base case
if (n == 1) {
printf("Move disk 1 from %c to %c\n", source, destination);
return;
}
// Recursive calls
towerOfHanoi(n - 1, source, destination, auxiliary);
printf("Move disk %d from %c to %c\n", n, source, destination);
towerOfHanoi(n - 1, auxiliary, source, destination);
}
int main() {
int n = 3; // Example: Tower with 3 disks
towerOfHanoi(n, 'A', 'B', 'C');
return 0;
} Output:
Move disk 1 from A to C
Move disk 2 from A to B
Move disk 1 from C to B
Move disk 3 from A to C
Move disk 1 from B to A
Move disk 2 from B to C
Move disk 1 from A to CThe program solves the Tower of Hanoi problem using recursion. It prints the sequence of moves required to move n disks from the source pole to the destination pole, using an auxiliary pole.
It breaks problem recursively to subproblems by moving n-1 disks to an auxiliary pole, transferring the remaining disk, and then moving back the n-1 disks to the destination pole.
4. C Program For Binary Search using Recursion
C Program:
#include <stdio.h>
int binarySearch(int arr[], int low, int high, int key) {
// Base case
if (low > high) {
return -1; // Element not found
}
int mid = (low + high) / 2;
if (arr[mid] == key) {
return mid; // Element found at index mid
} else if (arr[mid] > key) {
return binarySearch(arr, low, mid - 1, key); // Search in the left half
} else {
return binarySearch(arr, mid + 1, high, key); // Search in the right half
}
}
int main() {
int arr[] = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10};
int n = sizeof(arr) / sizeof(arr[0]);
int key = 7;
int result = binarySearch(arr, 0, n - 1, key);
if (result != -1) {
printf("Element %d found at index %d\n", key, result);
} else {
printf("Element %d not found in the array\n", key);
}
return 0;
} Output:
Element 7 found at index 6
The program shows binary search using recursion. It searches for a key in a sorted array and returns the index if the element is found, or -1 if it is not present.The search space is reduced to half each time based on arr[mid] and key.
Types of Recursion in C
In C programming, there are two main types of recursion:
- Direct Recursion
- Indirect Recursion.
1. Direct Recursion
Direct recursion is a type of recursion where a function calls itself. In direct recursion, the function directly invokes its own instance, creating a sequence of nested calls. Each recursive call works towards a base case, and the recursion unfolds in a straightforward manner when base case is met.
C Program Function to show direct recursion:
#include
void directRecursion(int n) {
if (n > 0) {
printf("%d ", n);
directRecursion(n - 1); // Recursive call
}
}
int main() {
printf("Direct Recursion Output: ");
directRecursion(5);
return 0;
} Output:
Direct Recursion Output: 5 4 3 2 1In above code
- The function
directRecursionprints the value ofnand makes a recursive call withn - 1. - The recursion continues until
nbecomes 0, printing values in decreasing order.
2. Indirect Recursion
Indirect recursion is a type of recursion where multiple functions call each other in a cycle. Instead of a single function calling itself, a group of functions cooperatively invokes one another. This creates an interconnected sequence of recursive calls, often leading to more complex patterns in the recursion process.
C Program Function to show Indirect recursion
#include
void functionA(int n);
void functionB(int n) {
if (n > 0) {
printf("%d ", n);
functionA(n - 1); // Call functionA
}
}
void functionA(int n) {
if (n > 0) {
printf("%d ", n);
functionB(n / 2); // Call functionB
}
}
int main() {
printf("Indirect Recursion Output: ");
functionA(10);
return 0;
} Output:
Indirect Recursion Output: 10 9 4 3 1In the above code
functionAandfunctionBcall each other in a cycle.- The output shows the sequence of values printed by both functions in a recursive manner.
What is the Difference Between Tailed And Non-Tailed Recursion?
| Basis | Tailed Recursion | Non-Tailed Recursion |
|---|---|---|
| Definition | The recursive call is the last thing executed by the function | The recursive call is followed by some computation after it returns |
| Stack usage | Only one stack frame is used at a time | One stack frame per recursive call is used, can cause stack overflow |
| Optimization | Can be optimized to iterative loops | Cannot be optimized, requires stack space for each call |
| Examples | Fibonacci, factorial | Tree traversal, quicksort |
Advantages and Disadvantages of Recursion in C
Advantages of Recursion in C:
- Simplicity and Readability: Recursive solutions often express the problem more elegantly and concisely, making the code easier to read and understand.
- Complex Problem Solving: Recursive algorithms can efficiently handle problems with complex, nested structures by breaking them down into simpler subproblems.
- Applicability to Certain Problems: Some problems are naturally recursive in nature, and using recursion to solve them can lead to more intuitive and straightforward code.
- Reduced Code Length: Recursive code can be shorter than iterative code for certain problems, reducing the overall length of the program.
- Dynamic Memory Allocation:Recursive functions can dynamically allocate memory as needed, facilitating more flexible data structures.
Disadvantages of Recursion in C:
- Stack Overflow: Recursive calls consume stack space, and if the depth of recursion is too large, it may lead to a stack overflow, causing the program to crash.
- Execution Overhead: Recursive calls typically incur more overhead than iterative solutions, leading to potentially slower execution.
- Memory Consumption: Each recursive call adds a new stack frame to the memory, potentially consuming a significant amount of memory for deeply nested recursion.
- Difficulty in Debugging: Debugging recursive code can be challenging due to the multiple levels of function calls and the dynamic nature of the call stack.
- Function Call Overhead: Function calls in C have some overhead, and in recursive solutions, this overhead is multiplied with each function call, impacting performance.
- Not Suitable for All Problems: Recursion may not be the most efficient or suitable approach for certain problems, particularly those that involve repetitive calculations or do not naturally decompose into smaller subproblems.
- Potential for Infinite Recursion: If not implemented carefully, recursion may lead to infinite loops, especially when a base case is not properly defined or reached.
Real World Applications of C Recursion
Here are some real-world examples of where recursion in C is commonly used:
- Binary search – Recursively divide the search space in half to find a value in a sorted array. The base case is an empty search space.
- Sorting algorithms – Quicksort, merge sort and heapsort can all be implemented recursively, dividing the data into smaller chunks to sort.
- Tree and graph traversal – Traverse nested tree data structures or graph networks recursively, visiting child nodes depth-first.
- Dynamic programming – Some DP solutions like Fibonacci build results from previous results, implemented through recursion.
- Backtracking algorithms – Recursively build potential solutions incrementally and abandon partial solutions that fail. Useful for puzzles like Sudoku.
- Mathematical problems – Factorial, GCD and other math problems can be solved elegantly with recursion and base cases.
- Fractals – Recursively draw fractals like the Koch snowflake by dividing the structure into self-similar smaller pieces.
- Towers of Hanoi – Move disks recursively between pegs, with each call handling fewer disks.
- File directory operations – Traverse or delete directories recursively to apply to all nested contents.
FAQ
What is recursion formula?
A recursion formula represents a mathematical relationship or sequence using a recursive definition. It defines a function in terms of its own previous values.
Why do we use recursion in C?
Recursion in C is employed to solve complex problems by breaking them into simpler, self-similar subproblems. It provides an elegant and concise way to express solutions for certain algorithms and problems, enhancing code readability and modularity.