Find Roots Of Quadratic Equation In Java

In this article, we will see find roots of Quadratic Equation in Java. We will see various percentage division program in java.So, Let’s dive in.

Problem Statement

Given the coefficients a, b, and c of a quadratic equation ax^2 + bx + c = 0, write a program to find the roots of quadratic equation in Java.

For Example

Input:

a = 1
b = 5
c = 6

Output:

Root 1 = -2
Root 2 = -3

Solution

Before moving towards the solution let’s first see how are the roots of quadratic equation calculated.

Calculating Roots Of Quadratic Equation

Steps to find the roots of a quadratic equation:

Step 1: Calculate the Discriminant, (D)

The discriminant of a quadratic equation is given by the formula:

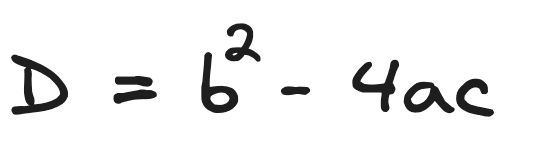
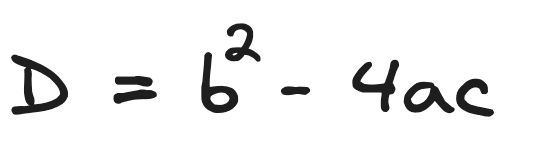
Where, (a), (b), and (c) are coefficients of the quadratic equation.

The discriminant (D), helps determine the nature of the roots of the equation.

Step 2: Determine the Number of Roots based on (D)

The value of the discriminant can determine the nature and number of roots:

1. If (D > 0): The quadratic equation has two distinct real roots.
2. If (D = 0): The quadratic equation has exactly one real root.
3. If (D < 0): The quadratic equation has no real roots which means roots are complex. 

Step 3: Use the Quadratic Formula to Find the Roots

The quadratic formula is a universal method for finding the roots of a quadratic equation. The formula is:

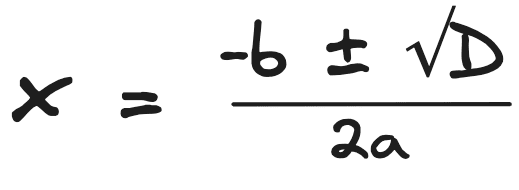
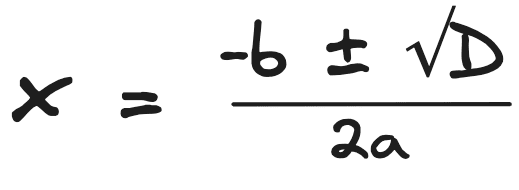
Where:

• x are the roots of the quadratic equation.
• (D) is the discriminant.
• The ± symbol indicates that there are usually two solutions: one for the positive square root and another for the negative square root.

So, based on the quadratic formula

If (D = 0), x = -b/2a

And if (D<0), since both the roots are complex and will be of form a+ib and a-ib. Here “a” is real part of roots and “b” is imaginary part of roots. Therefore:

Real part of roots: -b/(2a)

Imaginary part of roots: sqrt(-D)/(2a)

// Roots of quadratic equation program in java

import java.util.Scanner;

public class QuadraticEquation {

    public static void main(String[] args) {

        // Create Scanner object for user input
        Scanner scanner = new Scanner(System.in);
        
        // Prompt user for coefficients a, b, and c
        System.out.print("Enter coefficient a: ");
        double a = scanner.nextDouble();

        System.out.print("Enter coefficient b: ");
        double b = scanner.nextDouble();

        System.out.print("Enter coefficient c: ");
        double c = scanner.nextDouble();
        
        // Step 1: Calculate the discriminant, D
        double D = b * b - 4 * a * c;
        
        // Step 2: Determine the number of roots based on D
        if (D > 0) {
            // Two distinct real roots

            // Step 3: Use the quadratic formula
            double root1 = (-b + Math.sqrt(D)) / (2 * a);
            double root2 = (-b - Math.sqrt(D)) / (2 * a);

            // Output the roots
            System.out.println("Two distinct real roots: ");
            System.out.println("Root 1 = " + root1);
            System.out.println("Root 2 = " + root2);
        } 
        else if (D == 0) {
            // One real root (repeated)

            // Step 3: Use the quadratic formula
            double root = -b / (2 * a);

            // Output the root
            System.out.println("One repeated real root: ");
            System.out.println("Root = " + root);
        } 
        else {
            // Two complex conjugate roots

            // Real part of the root
            double realPart = -b / (2 * a);
            // Imaginary part of the root
            double imaginaryPart = Math.sqrt(-D) / (2 * a);

            // Output the roots
            System.out.println("Two complex roots: ");
            System.out.println("Root 1 = " + realPart + " + " + imaginaryPart + "i");
            System.out.println("Root 2 = " + realPart + " - " + imaginaryPart + "i");
        }
    }
}

Enter coefficient a: 1
Enter coefficient b: -3
Enter coefficient c: 2

Two distinct real roots: 
Root 1 = 2.0
Root 2 = 1.0

Key Takeaways

• Calculate the discriminant (D) to determine the nature and number of roots. The discriminant tells you if there are 2 real roots, 1 real root, or 2 complex roots.
• Use the appropriate formula based on the discriminant to find the roots:
  • If D > 0, use the quadratic formula to find 2 real roots
  • If D = 0, use -b/(2a) to find the 1 real root
  • If D < 0, split into real and imaginary parts to find complex roots
• Implement the logic in Java using if-else statements, based on the value of the discriminant. Calculate the roots using the appropriate formula in each branch.

Similar Posts

Add Days To The Current Date in Java

Calculate Area of Hexagon in Java

Program to Calculate EMI in Java

Calculate Area of a Circle in Java

Reverse A Number In Java

Student Percentage And Division Program

Checkout more Java Tutorials here.

I hope You liked the post ?. For more such posts, ? subscribe to our newsletter. Try out our free resume checker service where our Industry Experts will help you by providing resume score based on the key criteria that recruiters and hiring managers are looking for.

FAQ